Teoria Prismas

A área total do prisma é calculada pensando na planificação do prisma, isto é, a forma “recortada e desmontada do prisma”

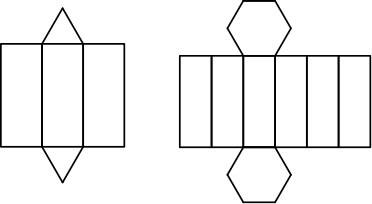
Note que independente do formato do prisma, a área total será calculada da seguinte maneira:

$$A_T = 2A_b + A_L$$

sendo que $2A_b$ representa duas áreas da base (sempre haverá os dois polígonos iguais) e $A_L$ é a área lateral será a união de retângulos (ou paralelogramos, no caso do prisma oblíquo).

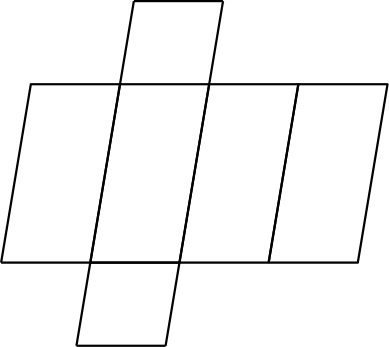
Vale ressaltar que cada tipo de prisma terá uma fórmula diferente para $A_b$, dependendo do seu formato.

Além disso, como é um cálculo de área, as unidades de medida serão $cm^2$, $m^2$, $km^2$ etc

O prisma reto ABCDEF possui os triângulos retângulos ABC e DEF como bases, como mostra a figura.

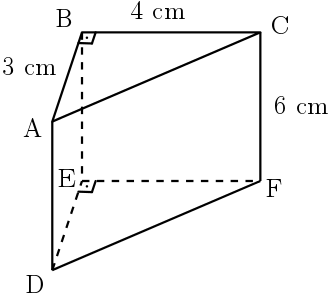
Vamos calcular sua área total.

Primeiro, veja que já podemos calcular a área das bases, pois são triângulos retângulos:

$$A_b = \dfrac{b \cdot h}{2} \\
A_b = \dfrac{3 \cdot 4}{2} \\
A_b = 6\ cm^2$$

Agora precisamos das áreas laterais, todas retangulares (ou seja, cuja área é $base \cdot altura$).

O retângulo ABED tem dimensões $3 \times 6$, ou seja:

$$3 \cdot 6 = 18\ cm^2$$

O retângulo BCFE tem dimensões $4 \times 6$, ou seja:

$$4 \cdot 6 = 24\ cm^2$$

Para obter a medida AC podemos aplicar o Teorema de Pitágoras:

$$AC^2 = 3^2 + 4^2 \\
AC^2 = 9 + 16 \\
AC^2 = 25 \\
AC = 5\ cm$$

Portanto a área ACFD é:

$$5 \cdot 6 = 30\ cm^2$$

Assim, a área total do prisma é:

\begin{align}
A_T &= 2 \cdot A_b + A_L \\
A_T &= 2 \cdot 6 + 18 + 24 + 30 \\
A_T &= 84\ cm^2
\end{align}