 Índice | Prismas
Índice | Prismas
Volume de prismas
Independente do formato da base do prisma, o volume dele sempre será calculado com a seguinte fórmula:
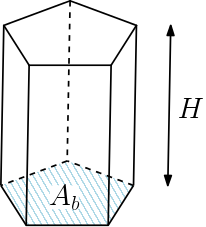
$$V = A_b \cdot H$$
Para o prisma oblíquo a fórmula é a mesma, só que, neste caso, a altura não tem a mesma medida que as arestas laterais.
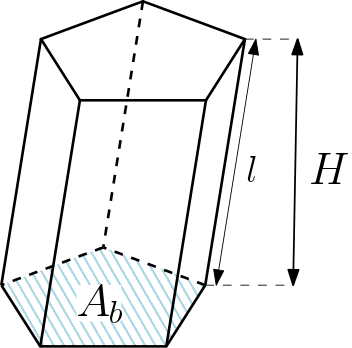
Obs.: Como é um cálculo de volume, as unidades serão $m^3$, $dm^3$, $cm^3$, entre outras, lembrando que há uma correspondência destas unidades com as unidades de capacidade (litro)
| 1 m³ | 1.000 L |
| 1 dm³ | 1 L |
| 1 cm³ | 1 mL |
Exemplo 1: como calcular volume de prisma
Neste exemplo vamos calcular o volume de um prisma reto cuja base é um triângulo equilátero de lado 4 cm e altura de 5cm:
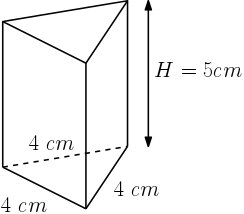
Como a fórmula do volume de prisma é:
$$V = A_b \cdot H,$$
precisamos calcular a área da base primeiro. Como o triângulo é equilátero, vamos usar a fórmula de área dele:
\begin{align}
A_{\Delta} &= \dfrac{l^2 \sqrt{3}}{4} \\
&= \dfrac{4^2 \sqrt{3}}{4} \\
&= 4\sqrt{3}\ cm^2
\end{align}
Agora levamos este resultado à formula do volume:
\begin{align}
V &= 4\sqrt{3} \cdot 5 \\
V &= 20 \sqrt{3}\ cm^3
\end{align}
Exemplo 2: cálculo da altura a partir do volume
Considere um prisma reto hexagonal que possui uma área da base de $40\ cm^2$. Se o volume do prisma é de $196\ cm^3$, qual é a altura deste prisma?
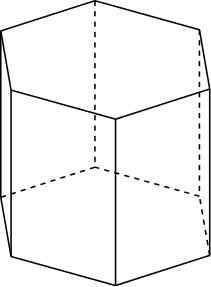
Então, ás vezes, os problemas já vão fornecer o volume e pedir outra medida. Vamos continuar usando a fórmula do volume e montar uma equação com ela, trocando as informações conhecidas.
Neste caso, já sabemos $V$ e $A_b$:
\begin{align}
V &= A_b \cdot H \\
196 &= 40 \cdot H \\
H &= \dfrac{196}{40} \\
H &= 4,9\ cm
\end{align}
Exemplo 3: misturando "metros" com litros
Uma empresa de decoração possui recipientes no formato de prisma reto cuja base possui $25\ cm^2$ de área e que serão preenchidos com água até a altura de $10\ cm$. Quantos destes vasos podem ser preenchidos com 1 L de água?
Primeiro vamos calcular o volume de cada recipiente, pois já temos a área da base deles e a altura:
$$V = A_b \cdot H \\
V = 25 \cdot 10 \\
V = 250\ cm^3$$
Agora, como comparar esta medida de volume com 1 litro?
A medida de $1 cm^3$ corresponde a $1\ mL$, portanto, em cada recipiente vão $250\ mL$. Podemos fazer uma regra de três então para ver quantos recipientes podem ser enchidos com $1\ L = 1000\ mL$ de água.
| Recipientes | Volume |
| 1 | 250 mL |
| x | 1000 mL |
$$250x = 1000 \\
x = \dfrac{1000}{250} \\
x = 4$$
Ou seja, com $1\ L$ de água podem ser preenchidos 4 recipientes.




