Teoria Pirâmide

Calcular a área total da pirâmide significa somar as áreas de todas as faces. É equivalente a calcular a área da figura formada pela planificação da pirâmide:

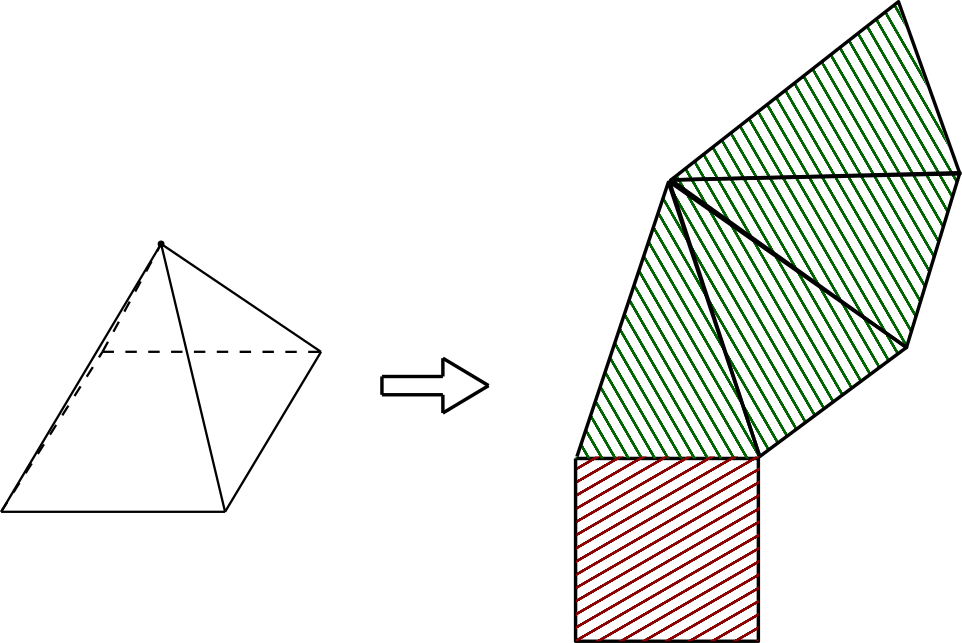
Repare que podemos separar a área total da pirâmide em duas partes: área lateral (formada pelos triângulos da lateral) e área da base. Portanto:

$$\boxed{A_T = A_L + A_b}$$

Sendo que:

$$\begin{cases}
A_T: \text{área total} \\
A_L: \text{área lateral} \\
A_b: \text{área da base}
\end{cases}$$

Obs.: se a pirâmide for regular, então a área lateral pode ser calculada da seguinte forma.

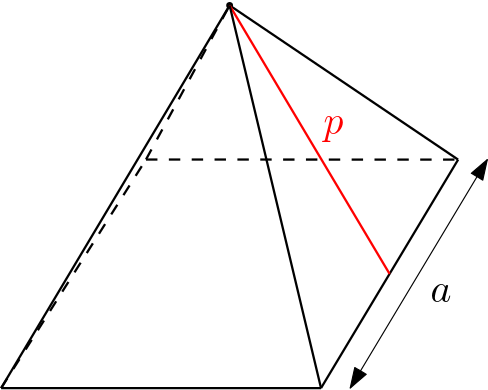
$$A_L = \dfrac{a \cdot p}{2} \cdot n$$

Sendo que $n$ é o número de lados da base.

Vamos utilizar como exemplo uma pirâmide de base quadrada de lado 6 cm e altura 4 cm, como na figura abaixo:

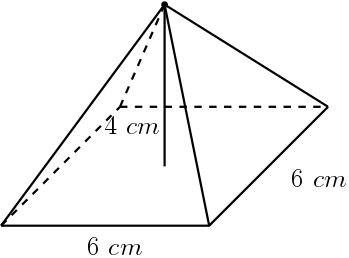
Para poder calcular a área total, precisamos da medida da apótema da pirâmide. Podemos construir o seguinte triângulo retângulo envolvendo a apótema:

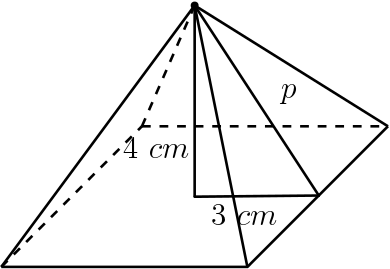
Vamos utilizar o Teorema de Pitágoras para calcular a apótema:

$$p^2 = 3^2 + 4^2 \\
p^2 = 9 + 16 \\
p^2 = 25 \\
p = \sqrt{25}\\
p = 5$$

Esta é a altura da face lateral. Precisamos dela para calcular a área lateral e assim a área total.

• Área de uma face lateral:

\begin{align}
A_F &= \dfrac{a \cdot p}{2} \\
A_F &= \dfrac{6 \cdot 5}{2} \\
A_F &= \dfrac{30}{2} \\
A_F &= 15\ cm^2
\end{align}

Agora para calcular a área lateral, basta multiplicar por 4, pois há 4 triângulos nas laterais:

• Área lateral

$$A_L = n \cdot A_F \\
A_L = 4 \cdot 15 \\
A_L = 60\ cm^2$$

Agora para a área total da pirâmide falta apenas a área da base, que neste caso é um quadrado:

$$A_b = l^2 \\
A_b = 6^2 \\
A_b = 36\ cm^2$$

• Área total:

$$A_T = A_L + A_b \\
A_T = 60 + 36 \\
A_T = 96\ cm^2$$