Teoria Pirâmide

A pirâmide possui medidas muito importantes que possuem relação entre si. Vamos mostrá-las usando uma pirâmide reta de base quadrada, mas a ideia se estende para qualquer tipo de base:

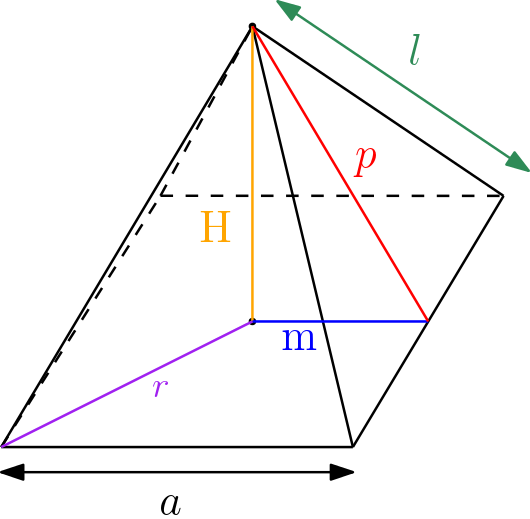
Sendo que, de maneira geral:

• $\color{orange}{H}$ (altura): distância do vértice da pirâmide até o plano da base;
• a: aresta da base;
• $\color{seagreen}{l}$: aresta lateral;
• $\color{blue}{m}$ (apótema da base) : segmento que une o centro da base até o ponto médio da aresta da base;
• $\color{red}{p}$ (apótema da pirâmide): segmento que une o vértice da pirâmide até o ponto médio da aresta da base – também é a altura da face lateral.
• $\color{purple}{r}$ (raio): distância do centro da base até um vértice da base.

Note que $H$, $m$ e $p$ formam um triângulo retângulo, ou seja, respeitam o Teorema de Pitágoras:

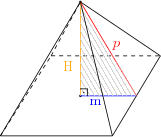
$$p^2 = H^2 + m^2$$

E também podemos montar outro triângulo retângulo com $r$ (o raio da pirâmide), $H$ (altura) e $l$ (aresta lateral):

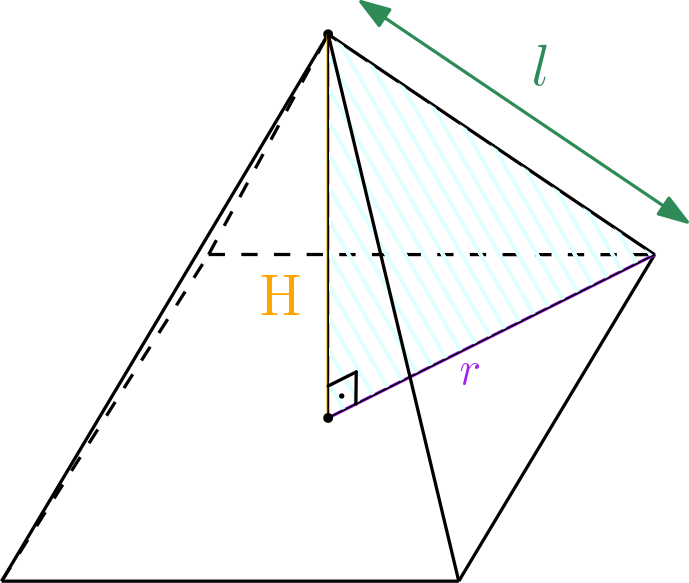
$$l^2 = r^2 + H^2$$

Iremos mostrar uma maneira de calcular a altura de uma pirâmide regular cujas arestas da base medem 4 cm e as arestas laterais medem 3 cm.

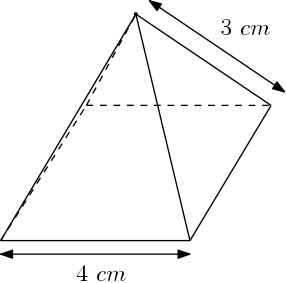
Já que temos a medida da aresta lateral, vamos obter o raio da pirâmide para poder construir um triângulo retângulo.

A diagonal de um quadrado pode ser calculada pela fórmula $d = a\sqrt{2}$, portanto, a diagonal da base mede:

$$d = 4\sqrt{2}\ cm$$

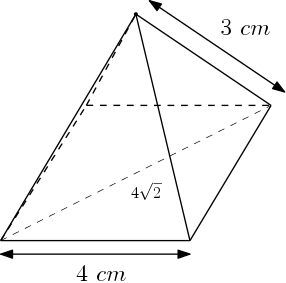
Assim, o raio é metade da diagonal:

$$r = \dfrac{4\sqrt{2}}{2} = 2\sqrt{2}\ cm$$

E considerando o triângulo retângulo formado pela altura, raio e aresta lateral temos:

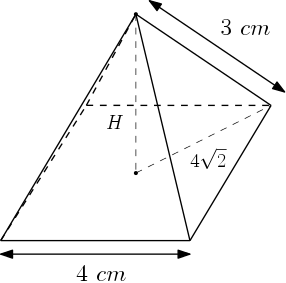
$$3^2 = (2\sqrt{2})^2 + H^2 \\
9 = 4\cdot 2 + H^2 \\
9- 8 = H^2 \\
H = \sqrt{1} \\
H = 1\ cm$$

Neste exemplo iremos calcular o apótema de uma pirâmide de base quadrada. A altura da pirâmide mede 8 cm e as arestas da base medem 12 cm.

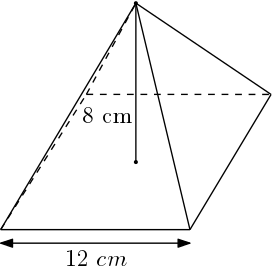
No caso da base quadrada, é simples: a medida do apótema da base é metade da medida do lado. Assim, com a altura, montamos um triângulo retângulo:

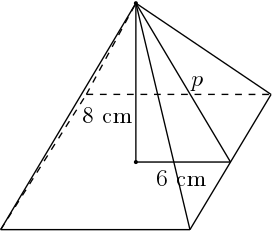
A apótema $p$ é a hipotenusa, portanto:

$$p^2 = 6^2 + 8^2 \\
p^2 = 36 + 64 \\
p^2 = 100 \\
p = \sqrt{100} \\
p = 10\ cm$$