Teoria Cubo e paralelepípedo

A área total do paralelepípedo vai ser calculada como a soma das áreas dos retângulos que compõe o paralelepípedo.

Vamos usar novamente o paralelepípedo de dimensões $a$, $b$ e $c$.

Note que há 2 retângulos de área $a \cdot b$:

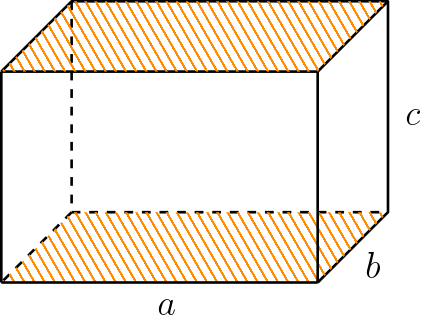
E também há 2 retângulos de área $b \cdot c$:

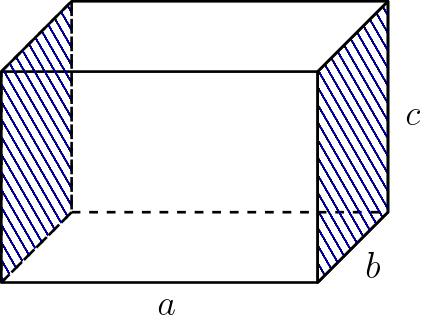
E 2 retângulos de área $a \cdot c$:

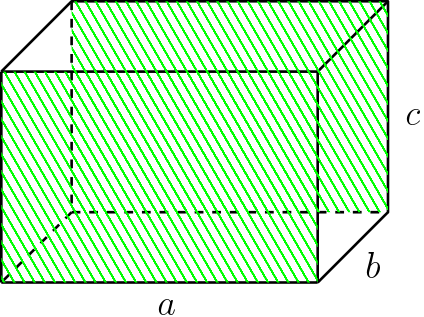
Portanto, a área total é:

$$A_T = 2ab + 2bc + 2 ac \\
A_T = 2 (ab + bc + ac)$$

Uma caixa será embrulhada com um papel de presentes, sendo que o papel deve recobrir totalmente cada face pelo menos uma vez. Se a caixa possui $60\ cm$ de comprimento, $25\ cm$ de largura e $30\ cm$ de comprimento, qual a menor área possível para o papel de presentes?

Este problema será resolvido calculando-se a área total da caixa. Para isso, vamos utilizar a fórmula que obtivemos:

\begin{align}
A_T &= 2 (ab + bc + ac) \\
A_T &= 2(60 \cdot 25 + 25 \cdot 30 + 60 \cdot 30) \\
A_T &= 2( 1500 + 750 + 1800) \\
A_T &= 2 \cdot 4050 \\
A_T &= 8100\ cm^2
\end{align}