Teoria Cubo e paralelepípedo

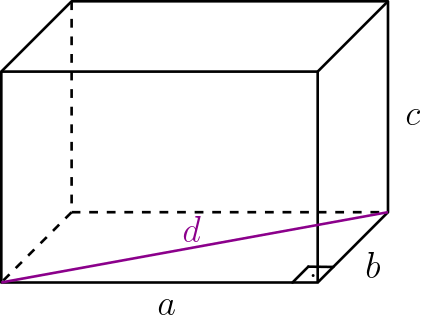
A diagonal do paralelepípedo é o segmento que liga dois vértices em faces opostas. Para calcular a diagonal do paralelepípedo de dimensões $a$, $b$ e $c$ vamos utilizar dois triângulos retângulos, sendo o primeiro no plano da base.

Primeiro vamos calcular a diagonal da base (é a hipotenusa do triângulo retângulo):

\begin{align}
d^2 = a^2 + b^2
\end{align}

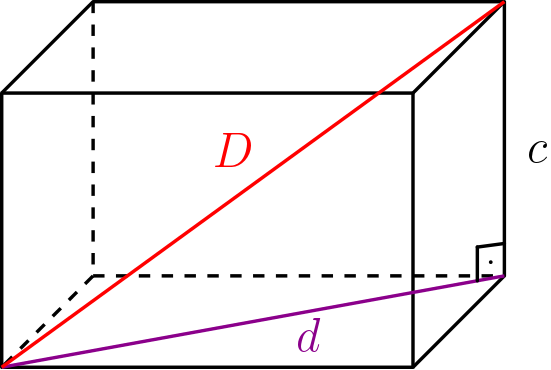
Não precisamos tirar a raiz quadrada, pois vamos utilizar o valor de $d^2$ no outro teorema de Pitágoras. O outro triângulo usa $d$ e $c$ como catetos e $D$ (a diagonal do paralelepípedo) é a hipotenusa:

\begin{align}
D^2 &= d^2 + c^2 \\
D^2 &= a^2 + b^2 + c^2 \\
D &= \sqrt{a^2 + b^2 + c^2}
\end{align}

Neste exemplo vamos calcular a diagonal de um paralelepípedo de $7\ cm$ de comprimento, $6\ cm$ de largura e $6\ cm$ de altura.

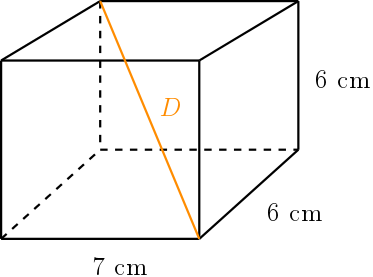
Vamos utilizar a fórmula que obtivemos:

\begin{align}
D &= \sqrt{6^2 + 6^2 + 7^2} \\
D &= \sqrt{36 + 36 + 49}\\
D &= \sqrt{121}\\
D &= 11\ cm
\end{align}