 Índice | Cubo e paralelepípedo
Índice | Cubo e paralelepípedo
Como calcular a diagonal do cubo
Considere um cubo com arestas medindo $a$. A seguir vamos calcular a medida de uma das diagonais da face deste cubo. Podemos fazer isso utilizando o teorema de Pitágoras, pois as faces são todas quadradas (com ângulos de $90^{\circ}$ nos vértices).
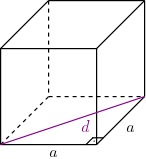
Neste caso estamos chamando a diagonal da face de $d$ (minúsculo) e ela é na hipotenusa do triângulo retângulo que montamos:
\begin{align}
d^2 &= a^2 + a^2 \\
d^2 &= 2a^2 \\
d &= \sqrt{2a^2} \\
d &= a\sqrt{2}
\end{align}
Porém, agora que estamos no mundo 3D é possível calcular uma outra diagonal, a que vai receber o nome de diagonal do cubo. É o segmento que liga um vértice do cubo ao vértice oposto, como na figura abaixo:
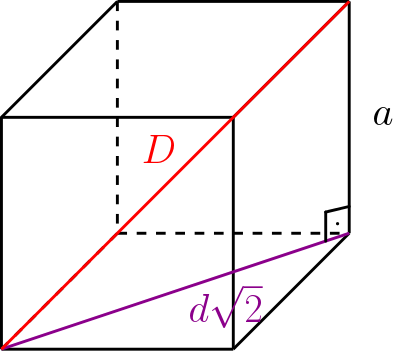
Neste caso chamamos a diagonal do cubo de $D$ (maiúsculo) e ela está na hipotenusa de um outro triângulo retângulo, cujos catetos medem $a$ e $a\sqrt{2}$. Vamos aplicar o Teorema de Pitágoras a este triângulo também:
\begin{align}
D^2 &= a^2 + (a\sqrt{2})^2 \\
D^2 &= a^ + a^2 \cdot 2 \\
D^2 &= a^2 + 2a^2 \\
D^2 &= 3a^2\\
D &= \sqrt{3a^2} \\
D &= a\sqrt{3}
\end{align}
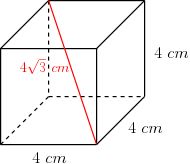
Exemplo: cálculo da diagonal do cubo
Se um cubo possui arestas de $4\ cm$, sua diagonal mede $4\sqrt{3}\ cm$.
Exemplo 2: cálculo da aresta a partir da diagonal
Considere um cubo ABCDEFGH, como na figura abaixo.
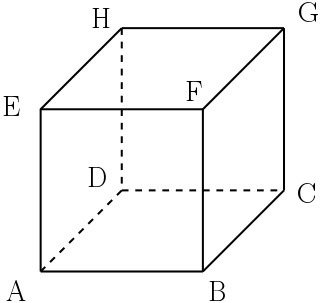
Se a distância entre os pontos E e C é de $6\ cm$, quanto medem as arestas do cubo?
A distância mencionada é justamente a diagonal do cubo. Então, sabendo que $D =a \sqrt{3}$ e que, no caso, $D = 6$, podemos usar a fórmula e calcular o valor da aresta:
$$D = a \sqrt{3} \\
6 = a \sqrt{3} \\
a = \dfrac{6}{\sqrt{3}}$$
Agora vamos nos lembrar do processo de racionalização:
$$a = \dfrac{6}{\sqrt{3}}^{\cdot \sqrt 3}_{\cdot \sqrt 3} = \dfrac{6\sqrt{3}}{3}\\
a = 2\sqrt{3}\ cm $$




