Teoria Cubo e paralelepípedo

Para calcular o volume do paralelepípedo, basta multiplicar as três dimensões (comprimento, largura e altura) entre si:

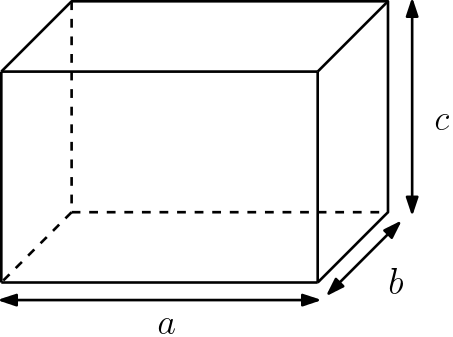
$$V = a \cdot b \cdot c$$

Quantos litros de água são necessários para encher uma piscina no formato de paralelepípedo retângulo com $25\ m$ de comprimento, $9\ m$ de largura e $2\ m$ de profundidade?

Vamos começar por calcular o volume da piscina:

$$V = a \cdot b \cdot c \\
V = 25 \cdot 9 \cdot 2 \\
V = 450\ m^3$$

Mas a medida foi obtida em metros cúbicos e, para o exemplo, queremos a medida em litros.

Basta lembrar de que $1\ m^3 = 1000\ L$, portanto:

$$V = 450 \cdot 1000 \\
V = 450.000\ L$$

Um aquário no formato de paralelepípedo retângulo está apoiado em uma face com $50\ cm$ de comprimento por $24\ cm$ de largura. Se forem despejados $36\ L$ de água dentro deste aquário, a água irá transbordar? Se não transbordar, qual altura o nível da água irá atingir? (Considere que o aquário possui $40\ cm$ de altura).

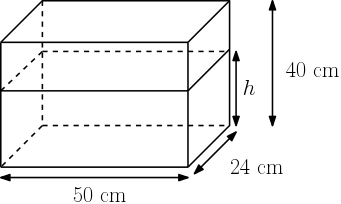
Neste exemplo já sabemos o volume mas falta uma das dimensões (a altura). O que vamos fazer então é montar uma equação com as informações baseada na fórmula do volume.

Mas há um detalhe: a medida de $36\ L$ não é compatível com as medidas em centímetros, pois $1\ cm^3 = 1\ mL$. Portanto, precisamos converter esta medida em mililitros primeiro:

$$36\ L = 36.000\ mL$$

Agora podemos montar a equação:

$$V = a \cdot b \cdot c \\
36000 = 50 \cdot 24 \cdot h \\
36000 = 1200h \\
h = \dfrac{36000}{1200} \\
h = 30\ cm$$

Portanto a água vai atingir a altura de $30\ cm$.