Teoria Trigonometria no ciclo trigonométrico

A medida da tangente de um ângulo no ciclo trigonométrico é definida a partir de um reta tangente ao ciclo trigonométrico, paralela ao eixo $y$.

Traçamos uma reta que liga o ponto do ciclo e a origem do sistema; vemos onde esta reta cruza a reta tangente; a tangente do ângulo será a distância (considerando sinal) deste ponto de cruzamento até o eixo horizontal.

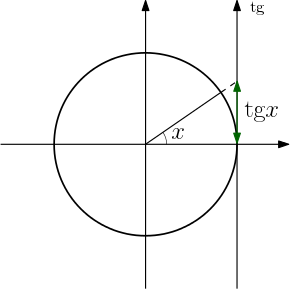
Além disso, vamos lembrar do triângulo formado por um ângulo no ciclo trigonométrico:

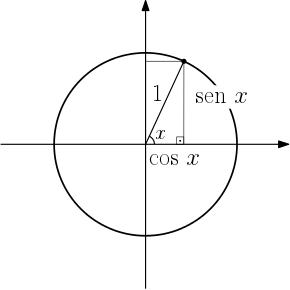
No triângulo retângulo a tangente pode ser calculada como:

$$\text{tg }x = \dfrac{cateto \ oposto}{cateto \ adjacente}$$

Aplicando isto ao triângulo do ciclo, podemos concluir que:

$$\boxed{\text{tg }x = \dfrac{\text{sen } x}{\cos x}}$$

Esta é a maneira alternativa de se calcular a tangente de um ângulo; também é uma ferramenta importante na simplificação de expressões ou funções trigonométricas.

A partir da definição que demos, podemos concluir que nos quadrantes I e III o sinal da tangente é positivo, pois a projeção bate na parte positiva da tangente.

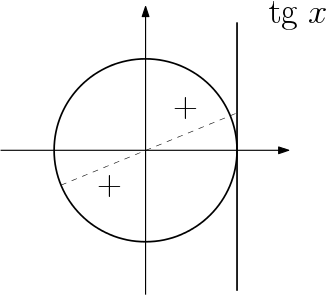
Nos quadrantes II e IV a projeção bate na parte negativa da tangente

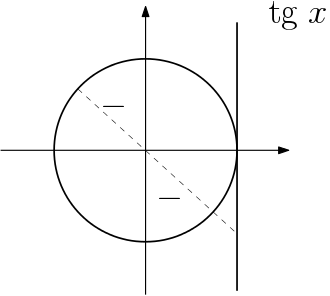
Então podemos resumir o sinal da tangente na seguinte figura.

Alguns ângulos não possuem medida de tangente; na primeira volta estes ângulos são $90^{\circ}$ e $270^{\circ}$.

A primeira explicação é que a reta que liga a origem ao ponto que determina estes ângulos é paralela à reta da tangente

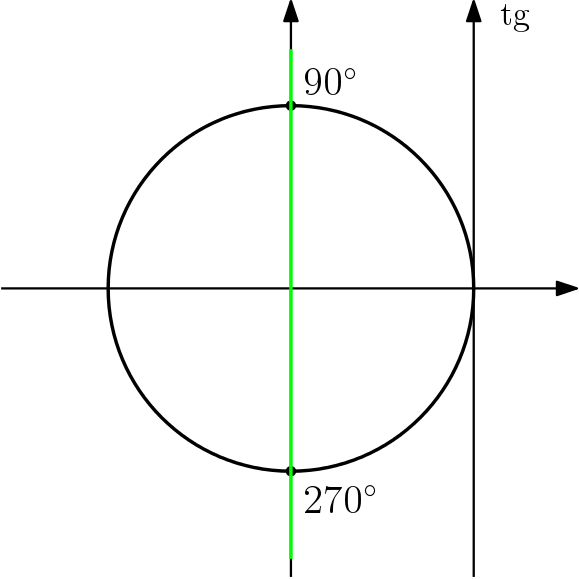
A outra explicação é algébrica: sabendo que $\cos 90^{\circ} = \cos 270^{\circ} = 0$ a expressão para a tangente com seno e cosseno fica impossível de ser calculada:

$$\text{tg }90^{\circ} = \dfrac{\text{sen }90^{\circ}}{\cos 90^{\circ}} = \dfrac{1}{0}$$

$$\text{tg }270^{\circ} = \dfrac{\text{sen }270^{\circ}}{\cos 90^{\circ}} = \dfrac{-1}{0}$$

Para os demais ângulos limite, a tangente é $0$:

$$\text{tg }0^{\circ} = \dfrac{\text{sen }0^{\circ}}{\cos 0^{\circ}} = \dfrac{0}{1} = 0$$

$$\text{tg }180^{\circ} = \dfrac{\text{sen }180^{\circ}}{\cos 180^{\circ}} = \dfrac{0}{-1} = 0$$

Podemos resumir isso na seguinte tabela:

O cálculo da tangente é semelhante ao de seno e cosseno, devemos seguir os mesmos passos:

• analisar o sinal de acordo com o quadrante;
• reduzir o ângulo para o 1º quadrante;
• calcular a tangente do ângulo do 1º quadrante.

Exemplos:

• $\text{tg }150^{\circ} =- \text{tg }30^{\circ} =- \dfrac{\sqrt 3}{3}$
• $\text{tg }225^{\circ} =+ \text{tg }45^{\circ} = 1$
• $\text{tg }300^{\circ} =- \text{tg }60^{\circ} =- \sqrt 3$