Teoria Trigonometria no ciclo trigonométrico

No ciclo trigonométrico, para qualquer ângulo $x$ podemos montar um triângulo retângulo em que os catetos medem $\cos x$ e $\text{sen }x $ e a hipotenusa mede $1$

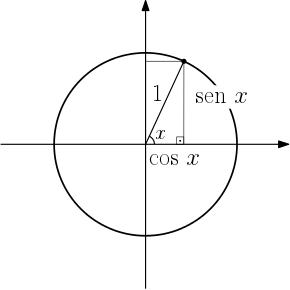
Aplicando o Teorema de Pitágoras neste triângulo obtemos a seguinte relação:

$$(\cos x)^2 + (\text{sen }x)^2 = 1^2 \\
\boxed{\cos^2 x + \text{sen}^2 x = 1}$$

Esta é uma equação (muito!) importante da trigonometria, que permite simplificar expressões ou funções trigonométricas e até calcular medidas trigonométricas de um ângulo sem nem conhecê-lo.

Obs.: o nome “identidade” usado para esta equação vem de “idêntico”, “igual”, não tem nada a ver com algum número de RG.

Sabendo que $90^{\circ}< \alpha < 180^{\circ}$ e que $\text{sen }\alpha = \dfrac{2}{3}$ iremos calcular $\cos \alpha$.

Vamos utilizar a identidade fundamental:

$$\text{sen}^2 x + \cos^2 x = 1 \\
\left ( \dfrac{2}{3} \right )^2 + \cos^2 \alpha = 1 \\
\dfrac{4}{9} + \cos^2 \alpha = 1 \\
\cos^2 \alpha = 1- \dfrac{4}{9} \\
\cos^2 \alpha = \dfrac{9- 4}{9} \\
\cos^2 \alpha = \dfrac{5}{9} \\
\cos \alpha = \pm \sqrt{\dfrac{5}{9}} \\
\cos \alpha = \pm \dfrac{\sqrt 5}{3}$$

Para decidir o sinal do cosseno, temos que levar em conta o quadrante do ângulo; como $\alpha$ está no quadrante $II$, o cosseno é negativo.

$$\cos \alpha =- \dfrac{\sqrt 5}{3}$$