Teoria Trigonometria no ciclo trigonométrico

Os ângulos negativos correspondem a giros no sentido horário do ciclo trigonométrico.

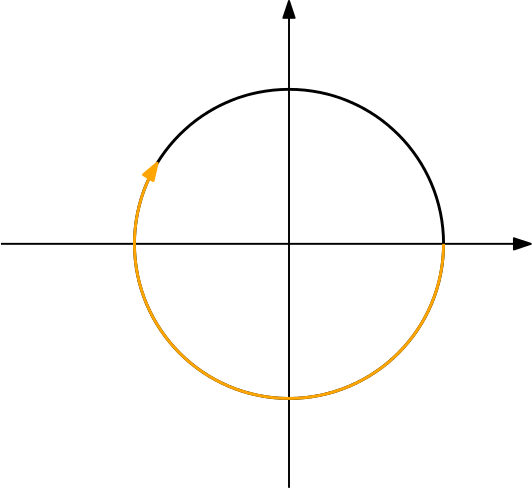
Além disso, cada ângulo negativo possui algum ângulo positivo congruente.

Considere um ângulo $x$ que esteja entre $-360^{\circ}$ e $0^{\circ}$. O ângulo positivo congruente a $x$ é $x + 360^{\circ}$.

$$x \rightarrow x + 360^{\circ}$$

Se o ângulo negativo for muito grande (menor que $-360^{\circ}$), primeiro dividimos por $360^{\circ}$ e depois somamos $360^{\circ}$ ao resto.

Exemplos de ângulos negativos maiores que $-360^{\circ}$:

• $-45^{\circ} \rightarrow 360- 45 = 315^{\circ}$
• $-180^{\circ} \rightarrow 360- 180 = 180^{\circ}$
• $-240^{\circ} \rightarrow 360- 240 = 120^{\circ}$
• $-300^{\circ} \rightarrow 360- 300 = 60^{\circ}$

Exemplos de ângulos negativos menores que $-360^{\circ}$:

• $-1020^{\circ}$

$$\begin{array}{c c}
1020 & | \hspace{-0.15em}\underline{\ \ 360 \ \ }\\
\hspace{-0.24em} \underline{-720 \,} & 2 \\
\hspace{0.75em} 300^{\circ}
\end{array}$$

Então: $-1020^{\circ} \rightarrow -300 + 360 = 60^{\circ}$

• $-1925^{\circ}$

$$\begin{array}{c c}
1925 & | \hspace{-0.15em}\underline{\ \ 360 \ \ }\\
\hspace{-0.64em} \underline{-1800 \,} & 5 \\
\hspace{0.75em} 125^{\circ}
\end{array}$$

Então: $-1925^{\circ} \rightarrow -125 + 360 = 235^{\circ}$