Teoria Trigonometria no ciclo trigonométrico

O ciclo trigonométrico é um ente matemático que possibilita o cálculo de medidas trigonométricas (seno, cosseno, tangente etc) para qualquer ângulo.

Ele é uma circunferência de raio $1$ centrada na origem.

O ponto $(1,0)$ é de onde começamos a medir os ângulos, sendo que sentido positivo é o anti-horário.

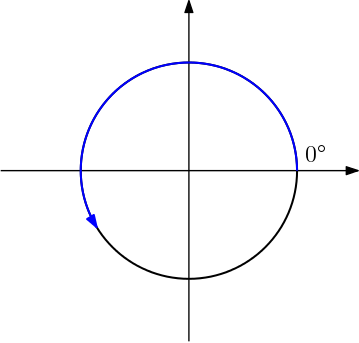
Os eixos delimitam 4 quadrantes no plano cartesiano, sendo que o primeiro quadrante fica em cima, à direita:

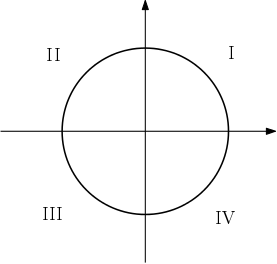
Agora vamos entender como esse negócio vai nos ajudar a determinar senos e cossenos.

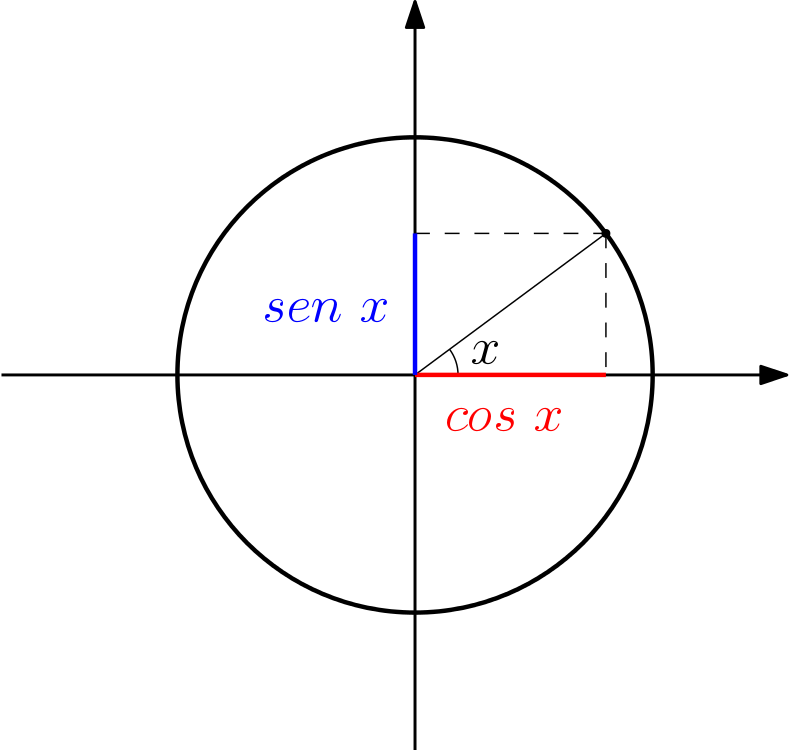
Vamos imaginar um ângulo $x$ a partir do centro. Este ângulo encontra um ponto do ciclo trigonométrico. A partir deste ponto fazemos uma projeção no eixo $x$ para construir um triângulo retângulo. A hipotenusa deste triângulo é $1$, pois é a medida do raio da circunferência. Vamos chamar seus catetos de $a$ e $b$.

Do triângulo retângulo temos que:

\begin{array}{l}
\text{sen }x = \dfrac{\text{cateto oposto}}{\text{hipotenusa}} = \dfrac{a}{1} = a\\
\cos x = \dfrac{\text{cateto adjacente}}{\text{hipotenusa}} = \dfrac{b}{1} = b
\end{array}

Isso significa que no ciclo trigonométrico:

• a projeção do arco no eixo $x$ determina o cosseno;
• a projeção do arco no eixo $y$ determina o seno.

É importante lembrar que estamos no plano cartesiano, então haverão medidas trigonométricas tanto positivas quanto negativas.