Você precisa de uma conta grátis
Você precisa de uma conta premium
Módulos
Para Ler
Vídeos
Exercícios do Matika
Perguntas
Suporte
Contato
Teoria Trigonometria no ciclo trigonométrico
Você está emTrigonometria no ciclo trigonométrico> Teoria
Compartilhe para promover uma educação melhor!
Índice | Trigonometria no ciclo trigonométrico
- 1O ciclo trigonométrico
- 2Sinais de seno e cosseno
- 3Ângulos maiores que $360^{\circ}$
- 4Ângulos negativos
- 5Redução ao primeiro quadrante
- 6Ângulos limite
- 7Cálculo de seno ou cosseno para qualquer ângulo
- 8A tangente no ciclo trigonométrico
- 9Identidade trigonométrica fundamental
- 10Outras razões trigonométricas
- 11Identidades trigonométricas
Precisa treinar?6
Ângulos limite
Os chamados ângulos limite são os ângulos que delimitam os quadrantes
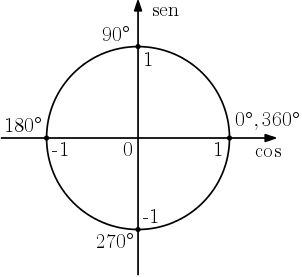
Lembrando que o raio do ciclo trigonométrico mede $1$, podemos obter as seguintes medidas de seno e cosseno para estes ângulos
| $0^{\circ}$ | $90^{\circ}$ | $180^{\circ}$ | $270^{\circ}$ | $360^{\circ}$ | |
| cos | $1$ | $0$ | $-1$ | $0$ | $1$ |
| sen | $0$ | $1$ | $0$ | $-1$ | $0$ |