Teoria Polinômios

O dispositivo de Briot-Ruffini é um algoritmo utilizado para dividir um polinômio $p(x)$ (de qualquer grau) por um polinômio de grau $1$, ou seja, na forma $ax+b$.

A seguir, veremos alguns exemplos para entender como o algoritmo funciona.

Iremos dividir $x^3 + 2x^2 + 3x + 4$ por $x+1$. Primeiro, é necessário calcular a raiz do divisor (obs.: este processo pode ser feito mentalmente)

$$x +1 = 0 \\ x=- 1$$

Este número será o pivô do método. A seguir dispomos os coeficientes do dividendo $1x^3 + 2x^2 + 3x + 4$ e o pivô da seguinte maneira:

1º passo: abaixar o primeiro coeficiente:

2º passo: multiplicar o pivô pelo coeficiente e somar ao próximo coeficiente; o resultado é colocado ao lado.

3º passo: repetimos o processo, agora com o resultado obtido no passo anterior.

4º passo: repetimos este processo até obter o último resultado.

5º passo: o último resultado é isolado, pois ele é o resto da divisão

6º passo: os outros números são os coeficientes do quociente da divisão. Como o dividendo possui grau $3$ e o divisor, grau $1$, então o quociente terá grau $3- 1 = 2$.

Assim, podemos escrever que:

$$\underbrace{x^3 + 2x^2 + 3x + 4}_{\text{dividendo}} = \underbrace{(x+1)}_{\text{divisor}} \cdot \underbrace{(x^2 + x + 2)}_{\text{quociente}} + \underbrace{2}_{\text{resto}}$$

Primeiro calculamos a raiz do divisor:

$$x- 2 = 0 \\ x = 2$$

Este será o pivô no método de Briot-Ruffini.

Repare que o polinômio possui grau $3$ e que o coeficiente de $x^2$ é $0$:

$$x^3 – 4x + 2 \equiv x^3 + 0x^2- 4x + 2$$

Assim, os números no método ficam da seguinte maneira:

1º passo: abaixar o primeiro coeficiente:

2º passo: multiplicar o pivô pelo coeficiente e somar ao próximo coeficiente; o resultado é colocado ao lado do primeiro valor.

3º passo: repetimos o processo, agora com o resultado obtido no passo anterior.

4º passo: repetimos este processo até obter o último resultado.

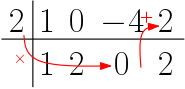
5º passo: o último resultado é isolado, pois ele é o resto da divisão

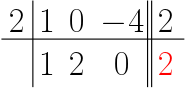
6º passo: os outros números são os coeficientes do quociente da divisão. Como o dividendo possui grau $3$ e o divisor, grau $1$, então o quociente terá grau $3- 1 = 2$.

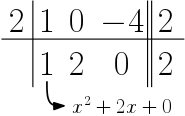
Assim, podemos escrever que:

$$x^3 – 4x + 2 = (x-2)(x^2 + 2x) + 2$$