Teoria Cônicas

Se em determinada elipse os parâmetros $a$ e $b$ forem iguais, então ela representa uma circunferência:

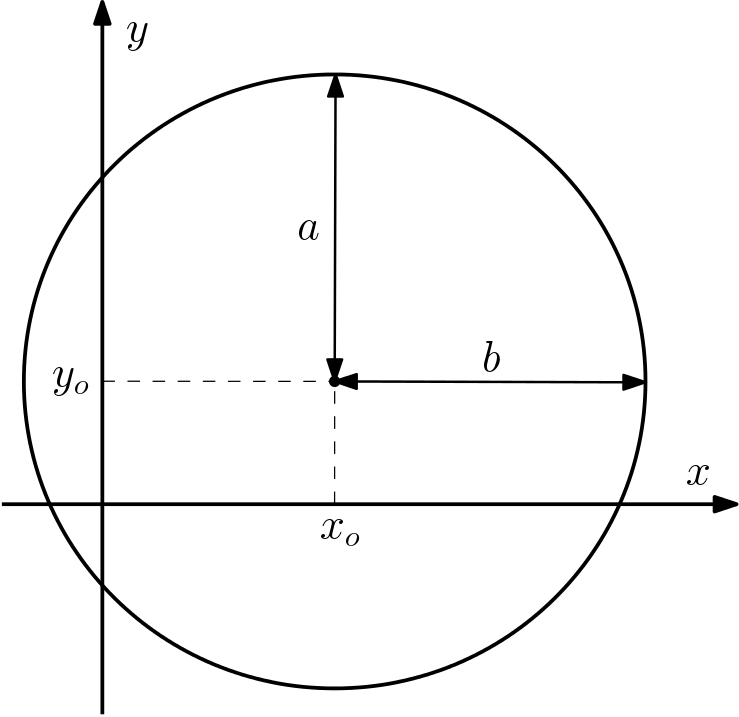
$$\dfrac{(x-x_o)^2}{a^2} + \dfrac{(y-y_o)^2}{a^2} = 1 \\
(x-x_o)^2 + (y-y_o)^2 = a^2$$

Podemos ver que a distância focal fica zerada neste caso:

$$a^2 = b^2 + c^2 \\
a^2 = a^2 + c^2 \\
c^2 = 0 \\
c = 0$$

Neste caso, dizemos que seus focos coincidem com o centro e os semi-eixos maior e menor são o raio da circunferência.

Além disso, a excentricidade da circunferência é nula:

$$e = \dfrac{c}{a} = \dfrac{0}{a} = 0$$