 Índice | Cônicas
Índice | Cônicas
- 1Elipse
- 2Equação reduzida da elipse
- 3Equação da elipse com centro fora da origem
- 4Excentricidade da elipse
- 5Caso especial da elipse: circunferência
- 6Hipérbole
- 7Equação reduzida da hipérbole
- 8Equação da hipérbole com centro fora da origem
- 9Excentricidade da hipérbole
- 10Parábola
- 11Equação reduzida da parábola
- 12Equação da parábola com vértice fora da origem
- 13Equação geral da cônica
Equação reduzida da elipse
A equação reduzida de uma elipse com centro na origem do sistema de coordenadas e focos no eixo $x$ é a seguinte:
$$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$$
Em que $a$ e $b$ são as medidas dos semieixos maior e menor, nesta ordem.
Se os focos estiverem no eixo $y$, então o parâmetro $a$ fica relacionado à variável $y$:
$$\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1$$
Conclusão: ao bater o olho em uma equação de elipse, iremos saber qual o eixo maior olhando qual variável tem o maior denominador, pois $a > b$.
A demonstração do porquê a equação é desta forma está a seguir, caso tenha curiosidade. Senão, pode ir direto para os exemplos de como utilizar a equação da elipse.
Desenvolvimento da equação da elipse com focos no eixo $x$
Vamos estudar primeiro a equação de uma elipse centrada na origem e com focos no eixo $x$.
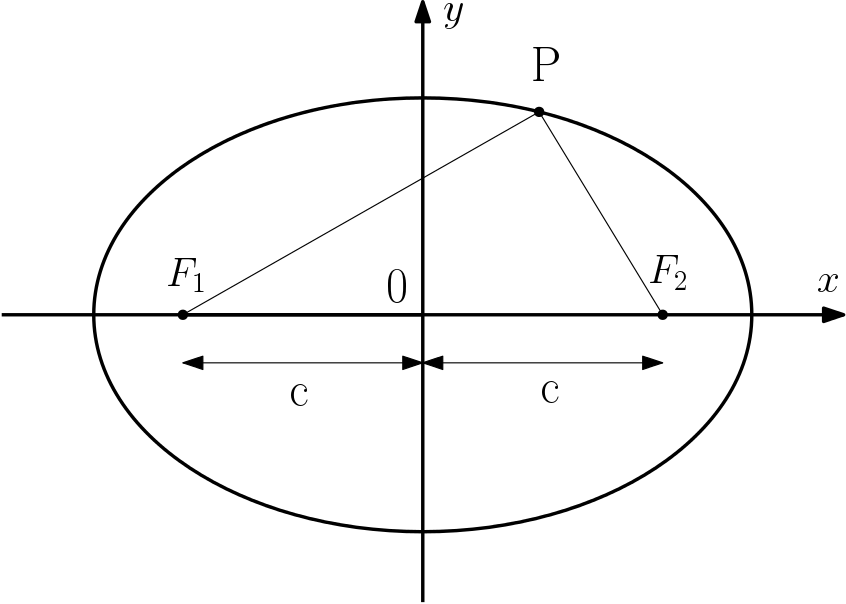
Assim, as coordenadas dos focos são $F_1 = (-c,0)$ e $F_2 = (c, 0)$, para $c > 0$. Vamos utilizar a definição e somar as distâncias de um ponto genérico $P=(x,y)$ até cada foco, sendo que o resultado deve ser $2a$.
Obs.: Lembre-se que a distância entre dois pontos $A=(x_a, y_a)$ e $B = (x_b, y_b)$ é calculada pela fórmula:
$$\boxed{d_{A,B} = \sqrt{(x_b- x_a)^2 + (y_b- y_a)^2}}$$
Então, no caso desta elipse a equação fica da seguinte forma:
$$d_{P,F_1} + d_{P,F_2} = 2a \\
\sqrt{(x+c)^2 + (y- 0)^2} + \sqrt{(x- c)^2 + (y-0)^2} = 2a \\
\sqrt{(x+c)^2 + y^2} + \sqrt{(x-c)^2 + y^2} = 2a$$
A fim de melhorar a equação, vamos isolar uma das raízes e elevar os dois lados da equação ao quadrado; do lado direito será necessário resolver um produto notável:
$$\sqrt{(x+c)^2 + y^2} = 2a- \sqrt{(x-c)^2 + y^2} \\
(\sqrt{(x+c)^2 + y^2})^2 = (2a- \sqrt{(x-c)^2 + y^2})^2 \\
(x+c)^2 + y^2 = 4a^2 – 4a \sqrt{(x-c)^2 + y^2} + (x-c)^2 + y^2$$
Vamos desenvolver os produtos notáveis para cancelar alguns termos iguais:
$$\color{blue}{x^2} + 2xc +\color{red}{c^2} + \color{green}{y^2} = 4a^2- 4a\sqrt{(x-c)^2 + y^2} + \color{blue}{x^2} – 2xc + \color{red}{c^2} + \color{green}y^2 \\
4xc = 4a^2- 4a\sqrt{(x-c)^2 + y^2}$$
Agora podemos simplificar os dois lados por $4$, isolar a raiz e novamente elevar os dois lados ao quadrado:
$$xc = a^2- a\sqrt{(x-c)^2 + y^2} \\
a\sqrt{(x-c)^2 + y^2} = a^2- xc \\
(a\sqrt{(x-c)^2 + y^2} )^2 = (a^2- xc)^2 \\
a^2((x-c)^2 + y^2) = a^4- 2a^2xc + x^2c^2 \\
a^2(x^2- 2xc + c^2 + y^2) = a^4- 2a^2xc + x^2c^2 \\
a^2x^2\color{blue}{- 2a^2xc} + a^2c^2 + a^2y^2= a^4\color{blue}{- 2a^2xc} + x^2c^2 \\
a^2x^2 + a^2c^2 +a^2y^2 = a^4 +x^2c^2$$
Aqui vamos substituir $c^2 = a^2- b^2$, equação vinda do triângulo retângulo que falamos anteriormente:
$$a^2x^2 +a^2 ( a^2 – b^2) + a^2y^2 = a^4 + x^2(a^2- b^2) \\
\color{red}{a^2x^2 +a^4}- a^2b^2 + a^2y^2 = \color{red}{a^2x^2 +a^4}- b^2x^2 \\
b^2x^2 + a^2y^2 = a^2b^2$$
Como $a$ e $b$ são valores não nulos, podemos dividir os dois lados da equação por $a^2b^2$:
$$\dfrac{b^2x^2}{a^2b^2} + \dfrac{a^2y^2}{a^2b^2} = \dfrac{a^2b^2}{a^2b^2} \\
\boxed{\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1}$$
Exemplo 1: como determinar a equação de uma elipse
Iremos determinar a equação da elipse representada no plano cartesiano abaixo, em que $F_1$ e $F_2$ são seus focos:
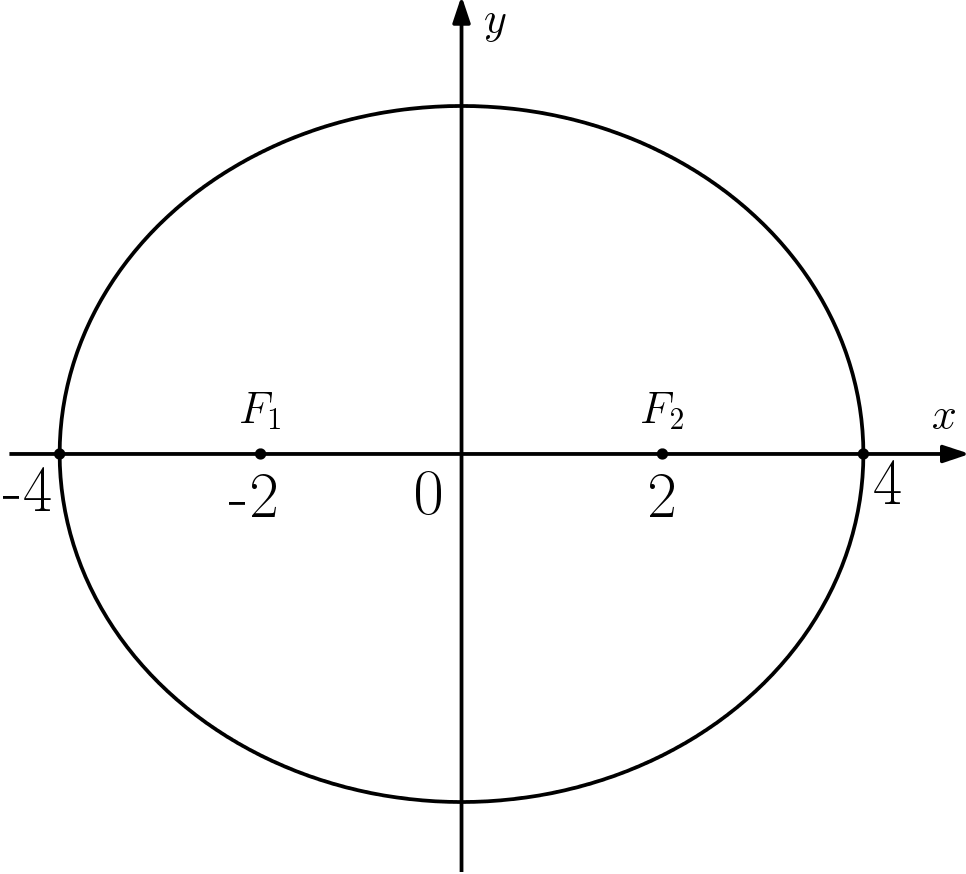
Pela imagem, vemos que $a = 4$ e que $c = 2$. Para determinar a equação precisamos da medida de $b^2$, que pode ser obtida pela relação:
$$a^2 = b^2 + c^2 \\
4^2 = b^2 + 2^2 \\
16 = b^2 + 4 \\
b^2 = 12$$
Portanto, a equação reduzida desta elipse é:
$$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \\
\dfrac{x^2}{16} + \dfrac{y^2}{12} = 1$$
Exemplo 2: como identificar pontos da elipse
Neste exemplo iremos utilizar a equação da elipse para determinar medidas e pontos importantes para a elipse.
Considere a elipse representada abaixo cuja equação é:
$$\dfrac{x^2}{9} + \dfrac{y^2}{4} = 1$$
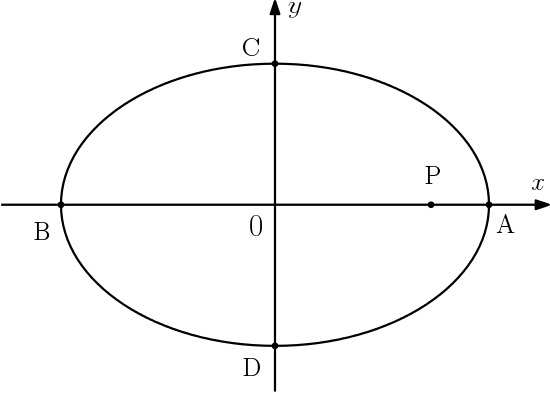
Determine:
a) As coordenadas dos vértices $A, B, C$ e $D$.
b) As coordenadas do ponto $P$, um dos focos da elipse.
a) Observando a equação, podemos concluir que:
$$a^2 = 9 \\
a = \sqrt{9} \\
a = 3$$
Então $A = (3,0)$ e $B = (- 3,0)$.
E também podemos obter a medida de $b$:
$$b^2 = 4 \\
b= \sqrt{4} \\
b = 2$$
Portanto $C = (0,2)$ e $D=(0,- 2)$.
b) As coordenadas de P dependem da medida $c$ da elipse; vamos calculá-la com a relação:
$$a^2 = b^2 + c^2 \\
9 = 4 + c^2 \\
c^2 = 5 \\
c = \sqrt{5}$$
Como $P$ está à direita da origem na figura, então $P = (\sqrt5, 0)$.
Exemplo 3: como utilizar a equação reduzida da elipse
Considere a elipse abaixo, que possui seus focos no eixo $y$ e contém o ponto $(-4,2)$.
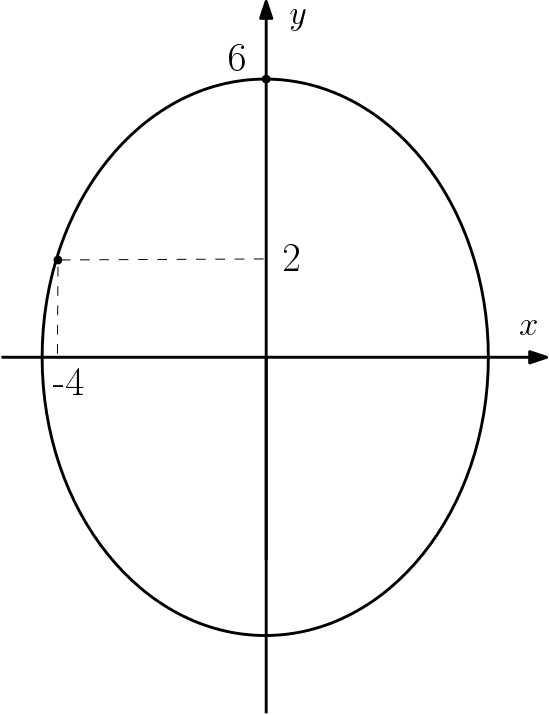
Iremos determine a equação reduzida desta elipse.
Como um vértice do eixo maior é $(6,0)$, podemos deduzir que $a = 6$. Portanto, a equação da elipse fica:
$$\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1 \\
\dfrac{x^2}{b^2} + \dfrac{y^2}{36} = 1$$
Agora, podemos substituir $x =-4$ e $y = 2$ para calcular o valor de $b^2$:
$$\dfrac{(- 4)^2}{b^2} + \dfrac{2^2}{36}= 1 \\
\dfrac{16}{b^2} + \dfrac{^1 4 \hspace{-0.55em}/}{^9 36 \hspace{-0.8em}/} = 1 \\
\dfrac{16}{b^2} = 1- \dfrac{1}{9} \\
\dfrac{16}{b^2} = \dfrac{9- 1}{9} \\
\dfrac{16}{b^2} = \dfrac{8}{9} \\
8b^2 = 144 \\
b^2 = \dfrac{144}{8} \\
b^2 = 18$$
Portanto a equação desta elipse é:
$$\dfrac{x^2}{18} + \dfrac{y^2}{36} = 1$$




