Teoria Cônicas

Outra cônica é conhecida como hipérbole. Ela não está tão presente no senso comum quanto a elipse, mas também é importante para a matemática.

Sua definição é a seguinte: dados dois focos $F_1$ e $F_2$, e uma constante positiva $2a$, a hipérbole é o conjunto formado pelos pontos $P=(x,y)$ tais que:

$$|d(P,F_1)- d(P,F_2)| = 2a$$

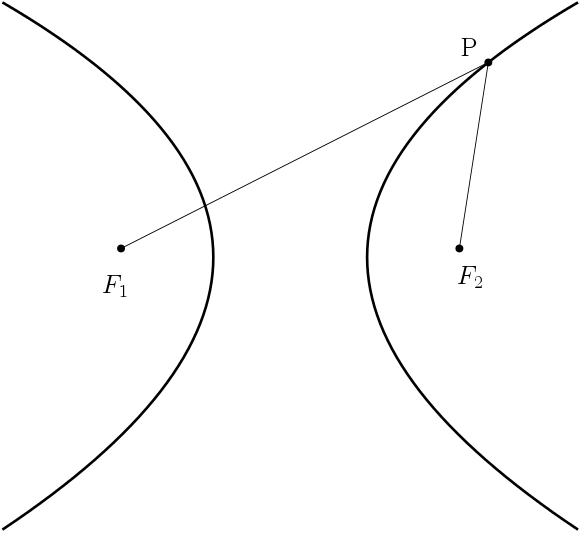
Ao contrário da elipse, o valor de $2a$ deve ser menor do que a distância entre os focos, chamada de $2c$.

$$2a < 2c$$

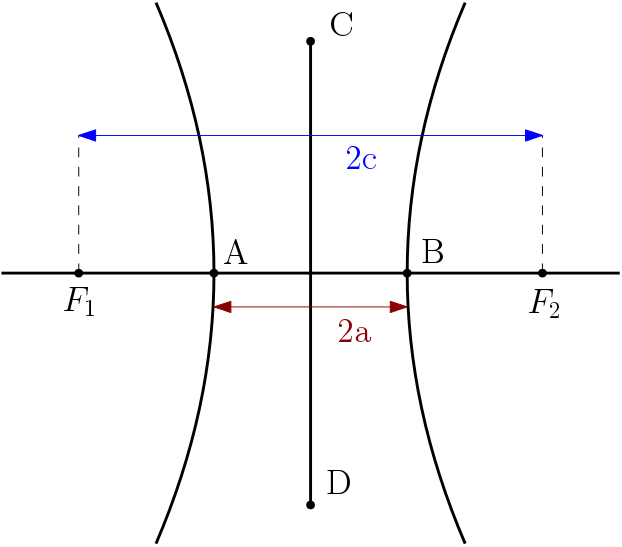
$F_1, F_2$: focos.
$O$: centro.
$A, B$: vértices.
$\overline{AB}$: eixo real.
$\overline{CD}$: eixo imaginário.
$\overline{F_1F_2}$: distância focal.

O eixo imaginário é o eixo perpendicular ao eixo real; a princípio os pontos $C$ e $D$ parecem arbitrários, mas eles possuem coordenadas específicas para cada hipérbole, como veremos abaixo.

Além destes nomes temos as seguintes medidas:

$$AB = 2a \\
CD = 2b \\
F_1F_2 = 2c$$

Com estas medidas construímos o seguinte triângulo retângulo:

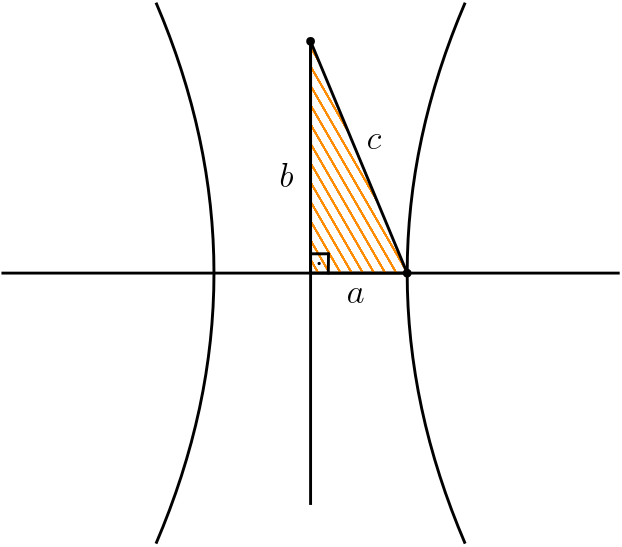
E portanto existe a seguinte relação entre as medidas da hipérbole:

$$\boxed{c^2 = a^2 + b^2}$$