Teoria Cônicas

Assim como a elipse e a circunferência, a hipérbole também possui excentricidade e é calculada da mesma maneira:

$$e = \dfrac{c}{a}$$

Neste caso, a excentricidade traduz se a hipérbole é “achatada” ou mais “aberta”.

Como sempre teremos $c > a$ na hipérbole, sua excentricidade sempre é um número maior que $1$.

Neste exemplo iremos calcular a excentricidade da hipérbole mostrada na figura abaixo, cujos focos e vértices estão destacados:

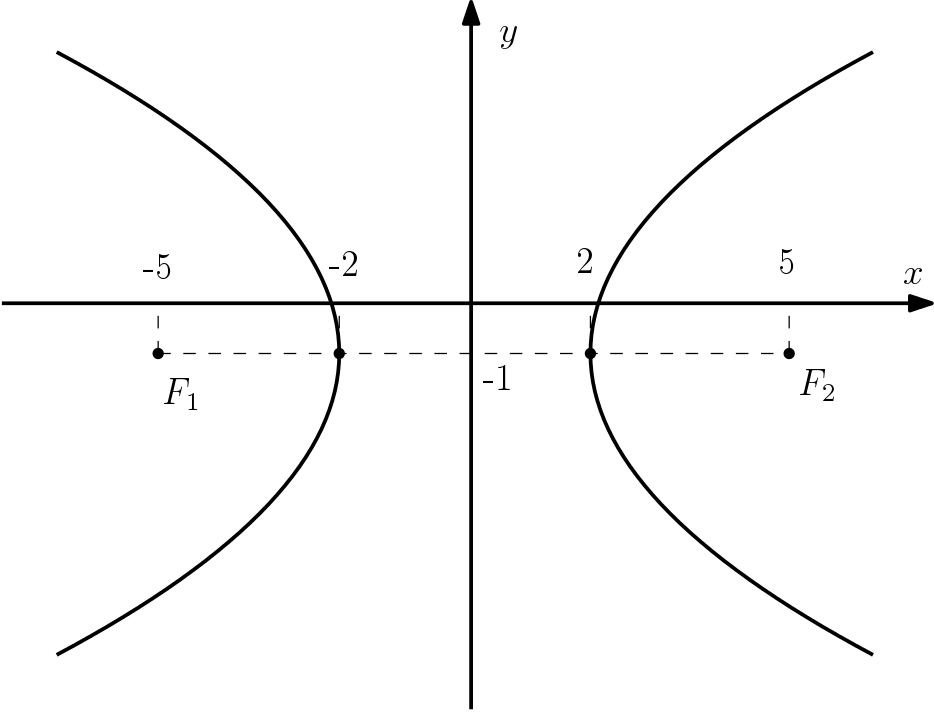
Pela figura, podemos perceber que $a = 2$ (distância do vértice até o centro) e que $c = 5$ (distância do foco até o centro).

Portanto:

$$e = \dfrac{5}{2} = 2,5$$

Considere uma hipérbole que tem distância focal de $26$ unidades, excentricidade $e = 2,6$, centro na origem e que possua o eixo $x$ como eixo real. Determine a equação reduzida desta cônica.

Se a hipérbole possui o eixo $x$ como eixo real e é centrada na origem, sua equação reduzida é da forma:

$$\dfrac{x^2}{a^2}- \dfrac{y^2}{b^2} = 1$$

Primeiro podemos calcular o parâmetro $c$, pois, segundo o enunciado, sabemos que $2c = 26$ (distância focal):

$$2c = 26 \\
c = 13$$

Agora vamos utilizar a excentricidade para achar o parâmetro $a$:

$$e = \dfrac{c}{a} \\
2,6 = \dfrac{13}{a} \\
a = \dfrac{13}{2,6} \\
a = 5$$

Para calcular o parâmetro $b$ basta utilizar a relação entre os parâmetros da hipérbole:

$$c^2 = a^2 + b^2 \\
13^2 = 5^2 + b^2 \\
169 = 25 + b^2 \\
b^2 = 144$$

Portanto a equação desta hipérbole é:

$$\dfrac{x^2}{25}- \dfrac{y^2}{144} = 1$$