 Índice | Cônicas
Índice | Cônicas
- 1Elipse
- 2Equação reduzida da elipse
- 3Equação da elipse com centro fora da origem
- 4Excentricidade da elipse
- 5Caso especial da elipse: circunferência
- 6Hipérbole
- 7Equação reduzida da hipérbole
- 8Equação da hipérbole com centro fora da origem
- 9Excentricidade da hipérbole
- 10Parábola
- 11Equação reduzida da parábola
- 12Equação da parábola com vértice fora da origem
- 13Equação geral da cônica
10
Parábola
Outro objeto de estudo das cônicas é a parábola. Geralmente ela é estudada como gráfico da função de 2º grau no Ensino Médio, o que não está errado, mas sua definição é geométrica. Portanto, utilizando a geometria analítica podemos explorar ao máximo esta figura, além de conhecer sua equação e seus pontos principais em várias situações.
A definição da parábola é: considere um ponto $F$, denominado foco da parábola, uma reta $r$ que não contém $F$, chamada de reta diretriz da parábola. A parábola é o conjunto dos pontos $P=(x,y)$ que equidistam de $F$ e de $r$.
$$d_{P,F} = d_{P, r}$$
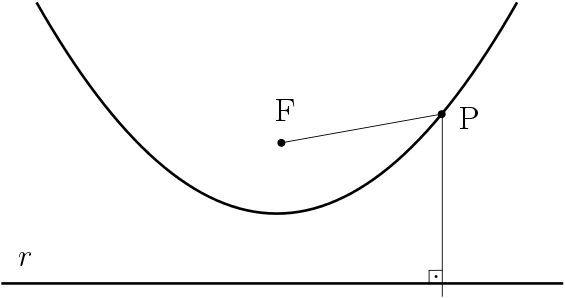
Esta distância é chamada de parâmetro da parábola.
10.1
Elementos da parábola
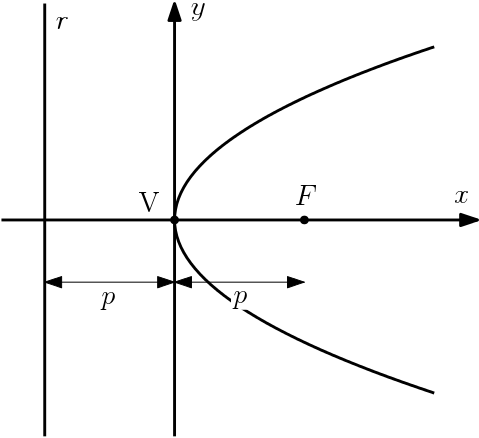
F: foco
r: reta diretriz
V: vértice
p: parâmetro




