Índice | Cônicas
Índice | Cônicas
- 1Elipse
- 2Equação reduzida da elipse
- 3Equação da elipse com centro fora da origem
- 4Excentricidade da elipse
- 5Caso especial da elipse: circunferência
- 6Hipérbole
- 7Equação reduzida da hipérbole
- 8Equação da hipérbole com centro fora da origem
- 9Excentricidade da hipérbole
- 10Parábola
- 11Equação reduzida da parábola
- 12Equação da parábola com vértice fora da origem
- 13Equação geral da cônica
Equação da elipse com centro fora da origem
Se o centro de uma cônica não for a origem, dizemos que a cônica está transladada.
Se o centro da elipse for o ponto $C=(x_o, y_o)$ e seu eixo maior for paralelo ao eixo $x$, então sua equação será:
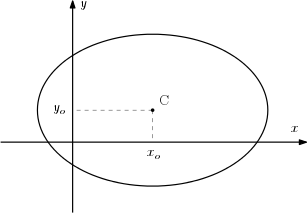
$$\dfrac{(x-x_o)^2}{a^2} + \dfrac{(y-y_o)^2}{b^2} = 1,$$
sendo que as definições de $a$ e $b$ são as mesmas: medidas dos semieixos maior e menor, respectivamente.
Sendo assim, podemos determinar as coordenadas dos vértices e dos focos. Considerando que o eixo maior é paralelo ao $x$, então as coordenadas dos focos são:
$$F_1 = (x_o- c, y_o) \\
F_2 = (x_o + c, y_o)$$
E os vértices $A, B, D$ e $E$, conforme mostrado na figura abaixo, tem coordenadas:
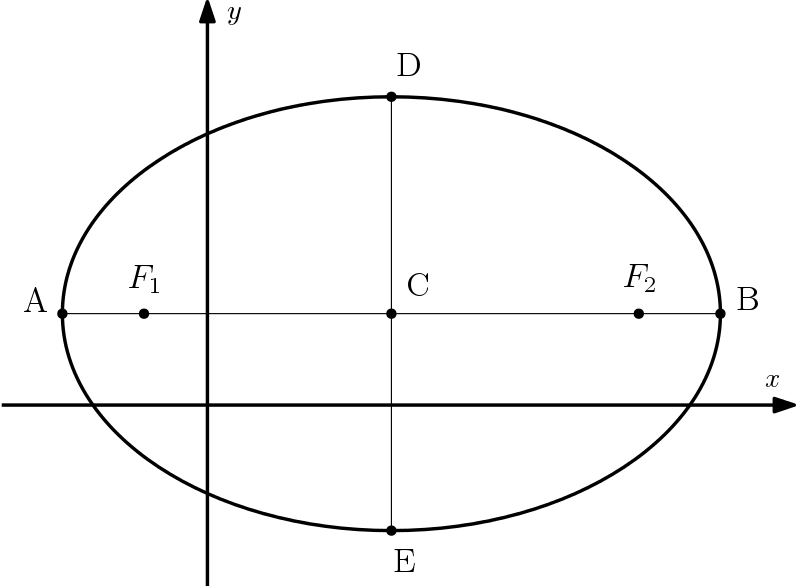
$$A = (x_o- a, y_o) \\
B = (x_o + a, y_o) \\
D = (x_o, y_o + b) \\
E = (x_o, y_o- b)$$
Se o eixo maior for paralelo ao eixo $y$, então sua equação é:
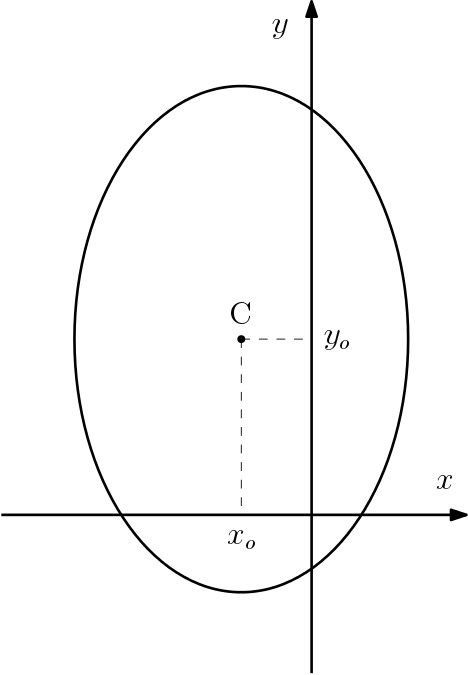
$$\dfrac{(x-x_o)^2}{b^2} + \dfrac{(y-y_o)^2}{a^2} = 1$$
E os focos e os vértices são encontrados de maneira análoga.
Vale notar que, em ambos os casos, o centro da elipse é o ponto médio entre os focos e também o ponto médio entre os vértices.
Exemplo 1: equação de elipse transladada
Considere uma elipse cujo centro é o ponto $(2,- 3)$, um de seus focos tem coordenadas $(2, 0)$ e um dos vértices é o ponto $(2,2)$. Neste exemplo iremos determinar sua equação.
Primeiro note que a reta que passa pelo centro e pelo foco é paralela ao eixo $y$, portanto seu eixo maior é paralelo ao $y$.
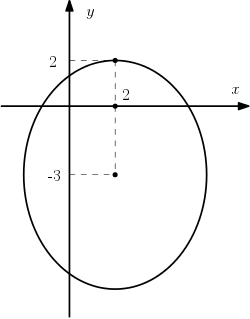
A distância entre o centro e o foco é a medida $c$, então:
$$c = 3$$
A distância entre o centro e o vértice do eixo maior é a medida $a$, portanto:
$$a = 5$$
Vamos utilizar a relação das medidas da elipse:
$$a^2 = b^2 + c^2 \\
5^2 = b^2 + 3^2 \\
25 = b^2 + 9 \\
b^2 = 16$$
Agora já podemos montar a equação reduzida desta elipse:
$$\dfrac{(x-x_o)^2}{b^2} + \dfrac{(y-y_o)^2}{a^2} = 1 \\
\dfrac{(x-2)^2}{25} + \dfrac{(y+3)^2}{16} = 1$$
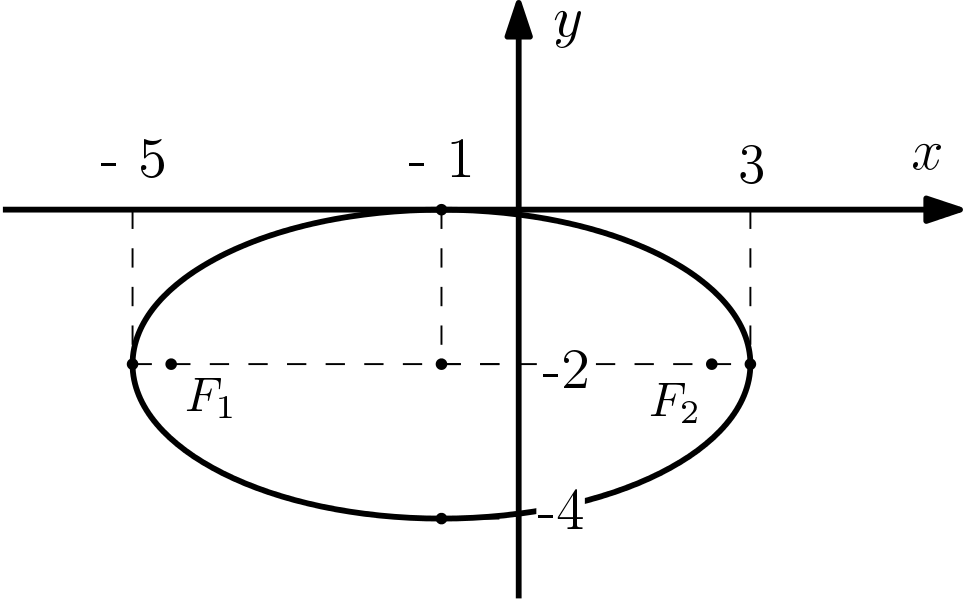
Exemplo 2: pontos da elipse transladada
Considere a elipse cuja equação é:
$$\dfrac{(x+ 1)^2}{16} + \dfrac{(y+2)^2}{4} = 1$$
Iremos determinar seu centro, focos e vértices.
O centro é facilmente identificado pelos valores que somam com $x$ e $y$, lembrando que devem ter o sinal trocado:
$$C = (-1, -2)$$
Podemos observar que o denominador do $x$ é maior, portanto o eixo maior é paralelo ao eixo $x$. Agora, vamos determinar os valores de $a$ e de $b$.
$$a^2 = 16 \\
a = 4$$
Como esta é a medida do semieixo maior, será somada/subtraída da coordenada $x$ do centro. Portanto os pontos:
$$(-1 + 4,- 2) = (3, – 2), \\
(-1- 4,- 2) = (-5,- 2),$$
são vértices da elipse.
Os outros vértices dependem da medida $b$, que será somada/subtraída à coordenada $y$ do centro:
$$b^2 = 4 \\
b = 2$$
Portanto os outros vértices são os pontos:
$$(- 1,- 2- 2) = (- 1,- 4) \\
(- 1,- 2 + 2) = (- 1, 0)$$
Agora falta apenas localizar os focos. Para isso precisamos da distância focal $c$; vamos utilizar a relação entre as medidas da elipse:
$$a^2 = b^2 + c^2 \\
16 = 4 + c^2 \\
12 = c^2 \\
c = \sqrt{12} \\
c = 2\sqrt{3}$$
Como o eixo maior é o eixo $x$, vamos somar/subtrair esta medida da coordenada $x$ do centro:
$$F_1 = (- 1- 2\sqrt{3},- 2 ) \\
F_2 = (- 1 + 2\sqrt{3},- 2)$$
Podemos até fazer um esboço desta elipse: