Índice | Cônicas
Índice | Cônicas
- 1Elipse
- 2Equação reduzida da elipse
- 3Equação da elipse com centro fora da origem
- 4Excentricidade da elipse
- 5Caso especial da elipse: circunferência
- 6Hipérbole
- 7Equação reduzida da hipérbole
- 8Equação da hipérbole com centro fora da origem
- 9Excentricidade da hipérbole
- 10Parábola
- 11Equação reduzida da parábola
- 12Equação da parábola com vértice fora da origem
- 13Equação geral da cônica
Equação da hipérbole com centro fora da origem
Se o centro da hipérbole for o ponto $C = (x_o, y_o)$ e seu eixo real for paralelo ao eixo $x$, então sua equação é a seguinte:
$$\dfrac{(x-x_o)^2}{a^2}- \dfrac{(y-y_o)^2}{b^2} = 1$$
Neste caso, para encontrar os vértices basta somar/subtrair a medida $a$ da coordenada $x$ do centro:
$$A = (x_o- a, y_o) \\
B = (x_o + a, y_o)$$
E fazemos o mesmo com a medida $c$ para encontrar os focos:
$$F_1 = (x_o- c, y_o) \\
F_2 = (x_o+c, y_o)$$
Caso o eixo real seja paralelo ao eixo $y$, então a equação é:
$$\dfrac{(y-y_o)^2}{a^2}- \dfrac{(x-x_o)^2}{b^2} = 1$$
Para encontrar os vértices, neste caso, somamos/subtraímos a medida $a$ da coordenada $y$ do centro:
$$A = (x_o, y_o- a) \\
B = (x_o, y_o + a)$$
E fazendo o mesmo para a medida $c$, encontramos os focos da hipérbole:
$$F_1 = (x_o, y_o- c) \\
F_2 = (x_o, y_o + c)$$
Vale lembrar que em qualquer caso, o centro é o ponto médio entre os focos da hipérbole e também ponto médio dos vértices da hipérbole.
Exemplo 1: equação de hipérbole transladada
Neste exemplo iremos determinar a equação da hipérbole representada na figura abaixo, cujos focos são $F_1$ e $F_2$:
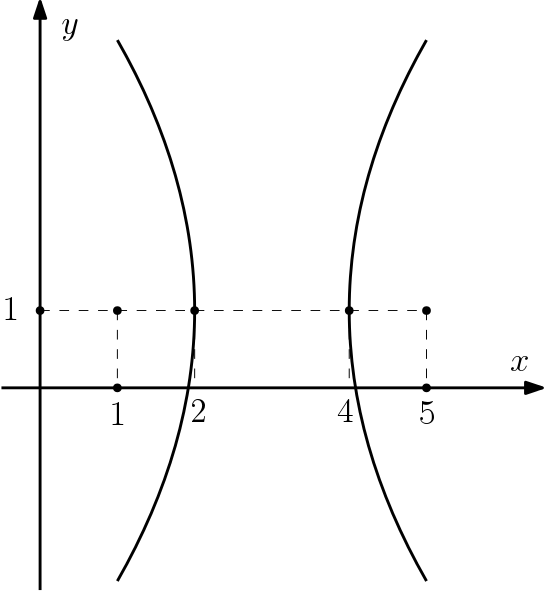
Primeiro, notamos que o eixo real da hipérbole é paralelo ao eixo $x$, então sua equação será da forma:
$$\dfrac{(x-x_o)^2}{a^2}- \dfrac{(y-y_o)^2}{b^2} = 1$$
Vamos começar determinando a medida $a$ da hipérbole através dos vértices; a medida $2a$ é definida como a distância entre os vértices, então:
$$2a = 2 \\
a = 1$$
A medida $2c$ é a distância entre os focos, portanto:
$$2c = 4 \\
c = 2$$
E agora utilizamos a relação entre as medidas da hipérbole:
$$c^2=a^2+b^2 \\
2^2 = 1^1 + b^2 \\
4 = 1 + b^2 \\
b^2 = 3$$
Agora só falta o centro da hipérbole, que é o ponto médio entre os focos:
$$C = \left ( \dfrac{1 + 5}{2}; \dfrac{1 + 1}{2}\right) \\
C = (3,1)$$
Portanto, a equação desta hipérbole é:
$$\dfrac{(x-3)^2}{1}- \dfrac{(y-1)^2}{3} = 1$$
Ou até podemos ignorar o denominador $1$:
$$(x-3)^2- \dfrac{(y-1)^2}{3} = 1$$
Exemplo 2: pontos da hipérbole transladada
Determine as coordenadas do centro, do foco e dos vértices de uma hipérbole cuja equação reduzida é:
$$\dfrac{(y-2)^2}{36}- \dfrac{(x-1)^2}{64} = 1$$
Começamos identificando o eixo real como sendo paralelo ao eixo $y$; isto vai ser importante na hora de identificar os pontos.
Depois, temos os valores de $a^2$ e de $b^2$, denominadores das frações da equação. Como $2a$ é a distância entre os vértices, vai nos ajudar a localizá-los.
$$a^2 = 36 \\
a = 6$$
O valor de $b$ só é importante para descobrir o de $c$, já que não ajuda a localizar nenhum ponto da hipérbole. Vamos então utilizar a relação entre as medidas da hipérbole:
$$c^2 = a^2 + b^2 \\
c^2 = 36 + 64 \\
c = \sqrt{100} \\
c = 10$$
Agora vamos identificar o centro para poder aplicar as distâncias $a$ e $c$. As coordenadas do centro somam com as variáveis $x$ e $y$, lembrando que estão com o sinal trocado. Assim,
$$C = (1, 2)$$
Agora vamos determinar os pontos.
Como o eixo real é paralelo ao eixo $y$, todas as distâncias serão somadas/subtraídas da coordenada $y$ do centro.
Os vértices serão:
$$A = (1, 2- a) = (1, 2- 6) = (1,- 4)\\
B = (1, 2+a) = (1,2+ 6) = (1, 8)$$
E os focos:
$$F_1 = (1,2- 10) = (1,- 9) \\
F_2 = (1, 2+ 10) = (1, 12)$$
Podemos até fazer um esboço desta hipérbole: