Teoria Cônicas

Se o vértice de uma parábola estiver transladado para um ponto de coordenadas $V = (x_o, y_o)$ e sua reta diretriz for paralela ao eixo $x$, então sua equação é:

$$(x-x_o)^2 = 4p(y- y_o)$$

Caso a reta diretriz seja paralela ao eixo $y$, então sua a equação é:

$$(y-y_o)^2 = 4p(x-x_o)$$

Neste exemplo iremos determinar a equação da parábola cujo vértice está no ponto $(-2, 1)$ e possui foco $(-2, 4)$, como na figura abaixo:

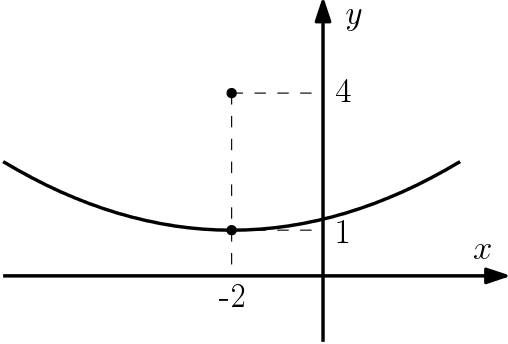
Primeiro notemos que a reta diretriz será paralela ao eixo $x$, portanto vamos usar a equação:

$$(x- x_o)^2 = 4p(y- y_o)$$

No caso, temos $x_o =- 2$ e $y_o = 1$, coordenadas do vértice. Como a distância entre o vértice e o foco é de $3$ unidades, então $p = 3$.

Portanto, a equação reduzida fica:

$$(x + 2)^2 = 4 \cdot 3(y- 1) \\
(x+2)^2 = 12(y-1)$$

Neste exemplo iremos determinar os principais elementos da parábola a partir de sua equação reduzida:

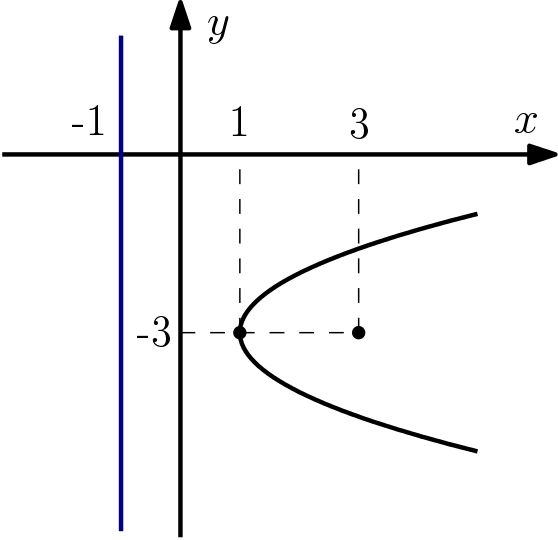
$$(y- 3)^2 = 8(x- 1)$$

Primeiro notamos que a reta diretriz é paralela ao eixo $y$, pois é ele que está elevado ao quadrado.

Segundo, podemos extrair as coordenadas do vértice pois são os números que somam com $x$ e $y$, lembrando de trocar o sinal.

$$V = (1,- 3)$$

Como a equação padrão é:

$$(y- y_o)^2 = 4p(x- x_o)$$

Podemos comparar com a equação que temos e notar que $4p = 8$, e que portanto:

$$4p = 8 \\
p = 2$$

Então, basta somar/subtrair este parâmetro do vértice para encontrarmos o foco e a reta diretriz.

$$F = (1 + 2,-3) = (3,-3) \\
r: \quad x = 1- 2 \rightarrow x =- 1$$

Então podemos até fazer um esboço da parábola: