Teoria Cônicas

Um das cônicas é a elipse. Muita gente já tem uma noção básica do formato da elipse, mas você sabe o que faz uma elipse ser uma elipse?

Ela é definida da seguinte maneira: dados dois pontos $F_1$ e $F_2$ (chamados de focos da elipse) e uma constante $2a$, a elipse é formada pelos pontos $P=(x,y)$ tais que:

$$d(P,F_1) + d(P,F_2) = 2a$$

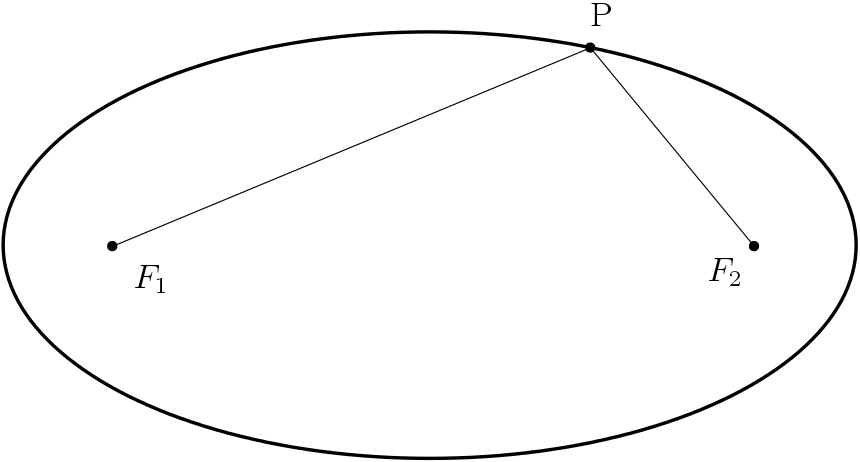
Obs.: A constante $2a$ deve ser maior do que a distância entre os focos, denotada por $2c$.

$$2a > 2c$$

Você deve estar se perguntado o porquê de definir constantes multiplicadas por 2. O motivo é que a metade destas medidas (no caso, $a$ e $c$) são importantes e muito utilizadas. Então, definimos desta maneira para facilitar as equações que vamos ver em breve.

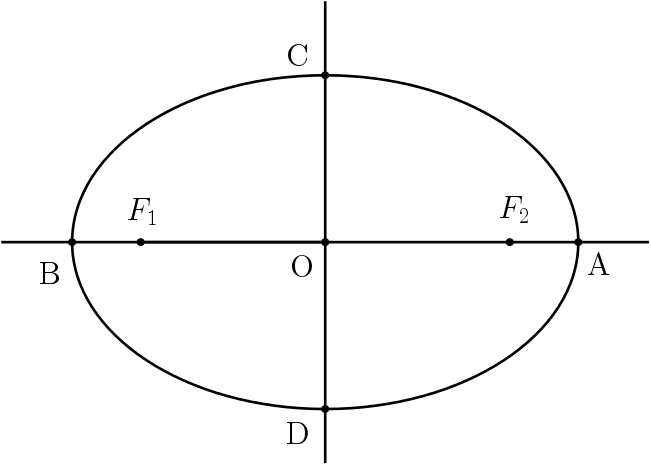
$F_1, F_2$: focos.
$O$: centro (ponto médio entre os focos).
$A, B, C, D$: vértices da elipse.
$\overline{AB}$: eixo maior.
$\overline{CD}$: eixo menor.
$\overline{F_1F_2}$: distância focal.

Além destes nomes, temos as seguintes medidas:

$$AB = 2a \\
CD = 2b\\
F_1F_2 = 2c$$

As medidas $2a$ e $2c$ vem desde a definição da elipse e agora, pelo gráfico da elipse, surge a medida $2b$.

A partir destas medidas é possível construir o seguinte triângulo retângulo:

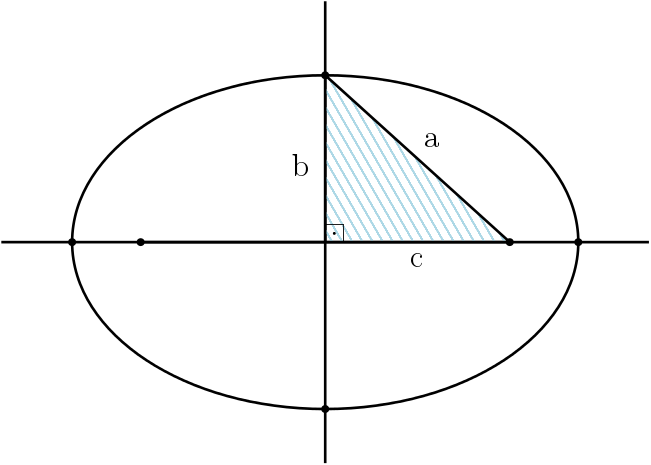
Portanto existe a seguinte relação entre as medidas da elipse:

$$a^2 = b^2 + c^2$$