Teoria Cônicas

Vamos passar as equações de parábola para situações padrão.

A equação de uma parábola com foco na parte positiva do eixo $x$ e reta diretriz paralela ao eixo $y$, com parâmetro $p$, é dada por:

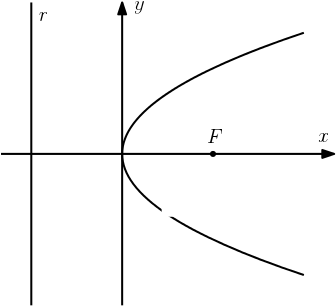
$$y^2 = 4px$$

Caso o foco fique na parte negativa do eixo $x$, isto é, a parábola fique virada para a esquerda, então a equação é:

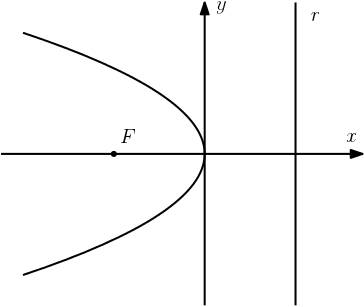
$$y^2 =- 4px$$

Se o foco estiver na parte positiva do eixo $y$ e a reta diretriz for paralela ao eixo $x$, com parâmetro $p$, então a equação é:

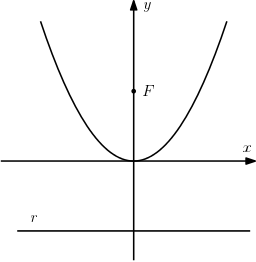
$$x^2 = 4py$$

Se o foco estiver na parte negativa do eixo $y$, isto é, a concavidade da parábola é virada para baixo, então sua equação é:

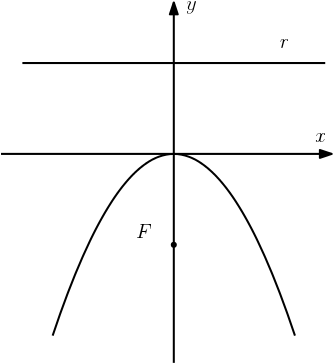
$$x^2=- 4py$$

Em seguida, iremos deduzir a primeira equação. Caso queira, pode pular direto para os exemplos, onde utilizamos estas equações.

Seja $F = (p,0)$ o foco da parábola e $x =- p$ a equação da reta diretriz da parábola. Assim, considere um ponto $P=(x,y)$ pertencente à parábola.

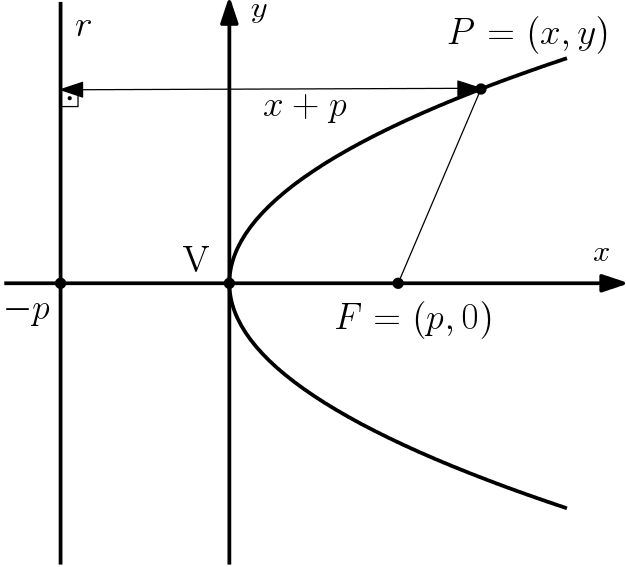
Pela figura, podemos notar que distância de $P$ à reta é $x+p$:

$$d_{P,r} = x + p$$

A distância de $P$ até $F$ pode ser calculada pela fórmula:

$$d_{P,F} = \sqrt{(x-p)^2 + (y- 0)^2}$$

Igualando estas duas distâncias, temos:

$$\sqrt{(x-p)^2 + (y- 0)^2} = x+p$$

Vamos elevar os dois lados ao quadrado e isolar $y^2$:

$$(\sqrt{(x-p)^2 + (y- 0)^2})^2 = (x+p)^2 \\
(x-p)^2 + y^2 = (x+p)^2 \\
x^2-2px + p^2 + y^2 = x^2 + 2px + p^2 \\
y^2 = 4px $$

A dedução da equação para foco no eixo $y$ é análoga.

Neste exemplo iremos determinar a equação da parábola abaixo, cuja reta diretriz é $x =- 3$ e foco $F = (3,0)$

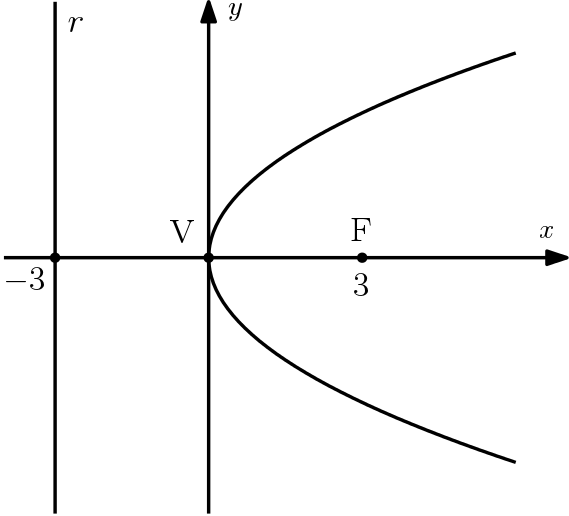
Como a distância entre o foco e o vértice é de 3 unidades, temos que:

$$ p = 3$$

Portanto:

$$y^2 = 4 \cdot 3 \cdot x \\
y^2 = 12x$$

Considere uma parábola com vértice na origem cujo foco seja o ponto $F = (0,2)$. Determine a equação da reta diretriz e a equação da parábola.

Podemos montar uma figura para deixar mais clara a situação

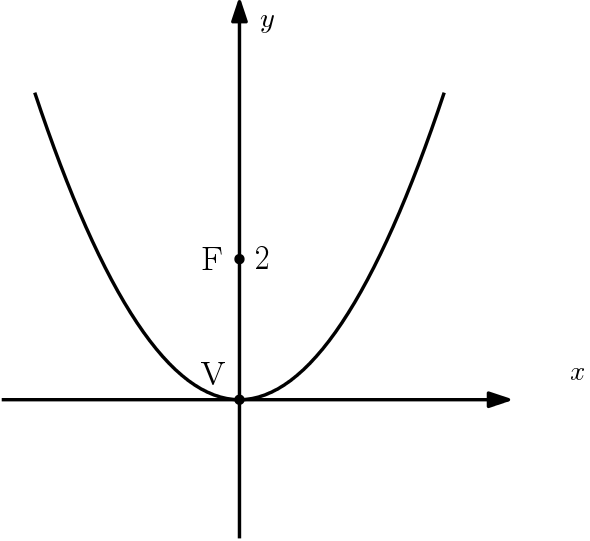
Podemos ver que $p = 2$, pois é distância do foco ao vértice. Como a distância do vértice até a reta diretriz deve ser 2 também, portanto a reta só pode ser $y =- 2$.

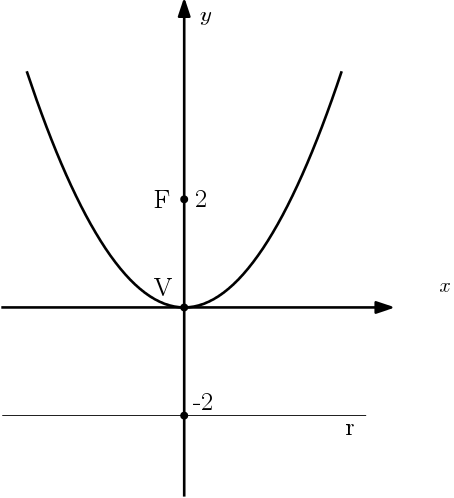
Além disso, temos sua equação é a seguinte:

$$x^2 = 4 \cdot 2 \cdot y \\
x^2 = 8y$$

Iremos identificar o foco de uma parábola cuja equação é:

$$3y^2- 8x = 0$$

Primeiro vamos deixar na forma reduzida, isto é, com o termo quadrático isolado (no caso, $y^2)$:

$$y^2 = \dfrac{8x}{3}$$

Podemos perceber que o eixo de simetria é o eixo $x$ e o vértice está na origem.

Agora, é só ver quem acompanha o termo linear (no caso, $x$) para saber quanto é $4p$; depois, vamos isolar o $p$.

$$4p = \dfrac{8}{3} \\
p = \dfrac{\frac{8}{3}}{4} \\
p = \dfrac{8}{3} \cdot \dfrac{1}{4} \\
p = \dfrac{2}{3}$$

Como o vértice é a origem, então podemos concluir que:

$$F = \left ( \dfrac{2}{3}, 0\right )$$

Neste exemplo iremos determinar a equação de uma parábola com vértice na origem e reta diretriz paralela ao eixo $x$ sabendo que esta reta passa pelo ponto $(6,- 3)$.

Se a parábola tem as características citadas no enunciado, então sua equação é da forma:

$$x^2 = 4py$$

Podemos substituir $x=6$ e $y=- 3$ para descobrir seu parâmetro:

$$6^2 = 4p (- 3) \\
36 =- 12p \\
p =- 3$$

Se o parâmetro é negativo, significa que a concavidade da parábola está ao contrário; neste caso, a parábola está com a concavidade para baixo e sua equação é:

$$x^2 =- 12y$$

Também podemos concluir que o foco está no ponto $(0,-3)$ e sua reta diretriz é dada pela equação $y = 3$.