Índice | Cônicas
Índice | Cônicas
- 1Elipse
- 2Equação reduzida da elipse
- 3Equação da elipse com centro fora da origem
- 4Excentricidade da elipse
- 5Caso especial da elipse: circunferência
- 6Hipérbole
- 7Equação reduzida da hipérbole
- 8Equação da hipérbole com centro fora da origem
- 9Excentricidade da hipérbole
- 10Parábola
- 11Equação reduzida da parábola
- 12Equação da parábola com vértice fora da origem
- 13Equação geral da cônica
Equação reduzida da hipérbole
Se os focos da hipérbole estiverem no eixo $x$ e seu centro for a origem, a equação reduzida da hipérbole é a seguinte:
$$\dfrac{x^2}{a^2}- \dfrac{y^2}{b^2} = 1$$
Em que $a$ é a medida do semieixo real e $b$ a medida do semieixo imaginário.
Se os focos estiverem no eixo $y$ então temos:
$$\dfrac{y^2}{a^2}- \dfrac{x^2}{b^2} = 1$$
Obs.: na hipérbole não é necessário que $a$ seja maior do que $b$. Então, ao bater o olho em uma equação, vamos saber qual o eixo real através dos sinais de $x^2$ e de $y^2$.
A dedução da equação reduzida da hipérbole é similar à da elipse.
Exemplo 1: como determinar a equação de uma hipérbole
Iremos determinar a equação reduzida da hipérbole mostrada abaixo, em que $F_1$ e $F_2$ são seus focos.
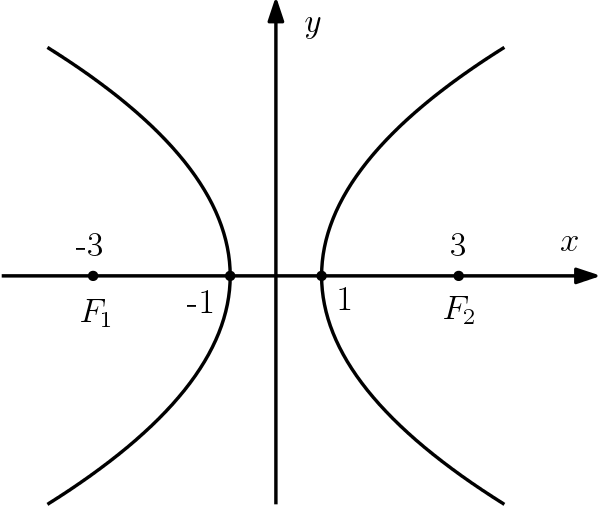
Pela figura podemos ver que $a = 1$ e que $c = 3$. Vamos utilizar a relação entre as medidas da hipérbole, pois precisamos de $b^2$ para completar a equação:
$$c^2 = a^2 + b^2 \\
3^2 = 1^2 + b^2 \\
9 = 1 + b^2 \\
b^2 = 8$$
Portanto, a equação reduzida desta hipérbole será:
$$\dfrac{x^2}{a^2}- \dfrac{y^2}{b^2} = 1 \\
\dfrac{x^2}{1} – \dfrac{y^2}{8} = 1 \\
x^2- \dfrac{y^2}{8} = 1$$
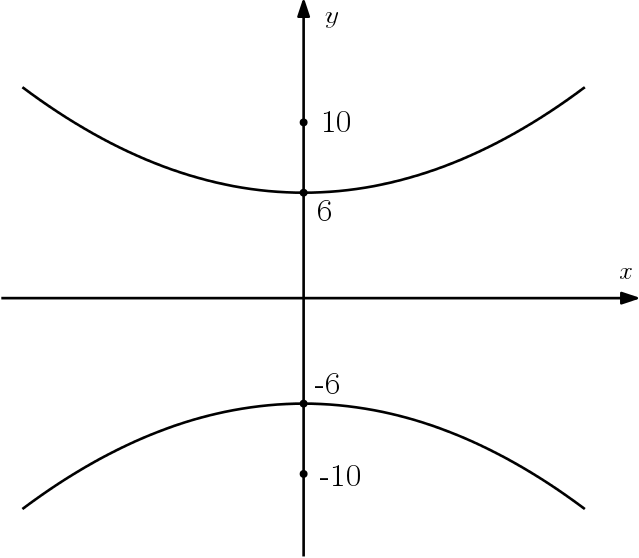
Exemplo 2: como identificar pontos da hipérbole
Considere a hipérbole cuja equação reduzida é:
$$\dfrac{y^2}{36}- \dfrac{x^2}{64} = 1$$
Iremos determinas as coordenadas de seus vértices e seus focos.
Primeiro note que o eixo real da hipérbole é o eixo $y$. Segundo, podemos obter as medidas de $a$, $b$ e $c$:
$$a^2 = 36 \\
a = \sqrt{36} \\
a = 6$$
$$b^2 = 64 \\
b = \sqrt{64} \\
b = 8$$
Agora utilizando a relação entre as medidas da hipérbole:
$$a^2 = b^2 + c^2 \\
a^2 = 36 + 64 \\
a = \sqrt{100} \\
a = 10$$
Então concluímos que seus vértices são $(0,8)$ e $(0,- 8)$.
Seus focos são $(0,10)$ e $(0,- 10)$.
Um esboço desta hipérbole seria